题目内容
已知函数f(x)="xlnx" (x 1)(ax a+1)(a∈R).
(1)若a=0,判断f(x)的单调性;.
(2)若x>1时,f(x)<0恒成立,求a的取值范围.
(1)单调减区间为(0,1),单调增区间为(1,+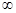 );(2)
);(2)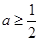 .
.
解析试题分析:(1)首先求导,然后根据导数的性质求出原函数的单调区间即可.
(2)设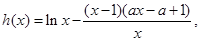 则a=0时,由(1)显然不成立;然后根据导函数的性质,求满足h(x)的最大值小于0的a的取值范围即可.(可分
则a=0时,由(1)显然不成立;然后根据导函数的性质,求满足h(x)的最大值小于0的a的取值范围即可.(可分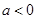 ,
,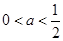 ,
,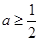 三种情况去验证.)
三种情况去验证.)
分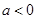 ,
,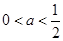 ,
,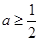 ,求
,求 时,h(x)的最大值小于0即可,
时,h(x)的最大值小于0即可,
试题解析:(1)若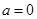 ,
, ,
,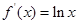
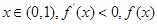 为减函数,
为减函数, 为增函数.
为增函数.
(2) 在
在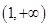 恒成立.
恒成立. 若
若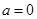 ,
, ,
,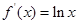
 为增函数.
为增函数.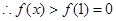
即 不成立;
不成立;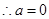 不成立.
不成立.
 ,
,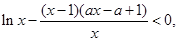 在
在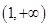 恒成立,
恒成立,
不妨设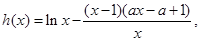
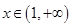
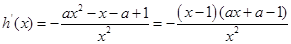 ,
,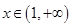
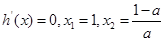 ,
,
若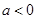 ,则
,则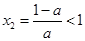 ,
,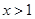 ,
,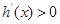 ,
,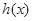 为增函数,
为增函数,
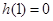 (不合题意);
(不合题意);
若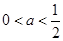 ,
, ,
,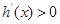 ,
,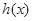 为增函数,
为增函数,
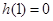 (不合题意);
(不合题意);
若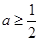 ,
, ,
,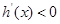 ,
,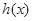 为减函数,
为减函数,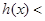
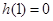 (符合题意).
(符合题意).
综上所述若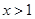 时,
时, 恒成立,则
恒成立,则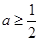 .
.
考点:1.函数的导数;2.单数的性质;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
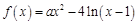 ,
,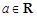 .
.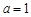 时,求
时,求 的单调区间;
的单调区间;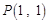 和函数
和函数 ,对任意
,对任意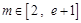 ,直线
,直线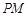 倾斜角都是钝角,求
倾斜角都是钝角,求 的取值范围.
的取值范围.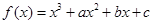 在
在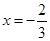 与
与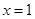 时都取得极值
时都取得极值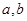 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式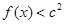 恒成立,求
恒成立,求 的取值范围
的取值范围 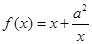 ,
, ,其中
,其中 .
. 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值; (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数 ,
, (
( )
) 中的任意实数x,在
中的任意实数x,在 上总存在实数
上总存在实数 ,使得
,使得 成立,求实数
成立,求实数 的取值范围
的取值范围 ,当
,当 在区间
在区间 内变化时,
内变化时,
 的取值范围;
的取值范围;
 有零点,求实数m的最大值.
有零点,求实数m的最大值.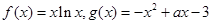 .
. 在
在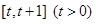 上的最小值;
上的最小值; 恒成立,求实数
恒成立,求实数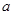 的取值范围;
的取值范围;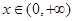 ,都有
,都有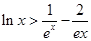 成立.
成立. .
. 的图象在
的图象在 处的切线方程;
处的切线方程; 对任意的
对任意的 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. .
. 且
且 时,证明:
时,证明: ;
; ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 时,证明:
时,证明: .
.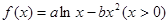 ,若函数
,若函数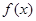 在
在 处与直线
处与直线 相切,
相切,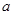 ,
, 的值;(2)求函数
的值;(2)求函数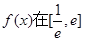 上的最大值.
上的最大值.