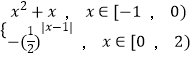题目内容
【题目】已知直线l的参数方程: ![]() (t为参数),曲线C的参数方程:
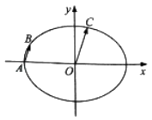
(t为参数),曲线C的参数方程: ![]() (α为参数),且直线交曲线C于A,B两点.
(α为参数),且直线交曲线C于A,B两点.
(Ⅰ)将曲线C的参数方程化为普通方程,并求θ= ![]() 时,|AB|的长度;
时,|AB|的长度;
(Ⅱ)已知点P:(1,0),求当直线倾斜角θ变化时,|PA||PB|的范围.
【答案】解:(Ⅰ)曲线C的参数方程: ![]() (α为参数),曲线C的普通方程为
(α为参数),曲线C的普通方程为 ![]() .
.
当θ= ![]() 时,直线AB的方程为,y=x﹣1,
时,直线AB的方程为,y=x﹣1,
代入 ![]() ,可得3x2﹣4x=0,∴x=0或x=
,可得3x2﹣4x=0,∴x=0或x= ![]()
∴|AB|= ![]()
![]() =
= ![]() ;
;
(Ⅱ)直线参数方程代入 ![]() ,得(cos2θ+2sin2θ)t2+2tcosθ﹣1=0.
,得(cos2θ+2sin2θ)t2+2tcosθ﹣1=0.
设A,B对应的参数为t1,t2,∴|PA||PB|=﹣t1t2= ![]() =
= ![]() ∈[
∈[ ![]() ,1].
,1].
【解析】(1)由同角三角函数关系进行消参,得到曲线C的普通方程,当θ=![]() 时,直线AB的方程为,y=x﹣1,由弦长公式可解得|AB|,(2)由t的几何意义可得出|PA||PB|的范围.
时,直线AB的方程为,y=x﹣1,由弦长公式可解得|AB|,(2)由t的几何意义可得出|PA||PB|的范围.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目