题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:依题意 由于 由于直线
因此 |
(2) |
解:当 证明:当 当 ∴ |
(3) |
解:由于
综上知对正整数 |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
| |||||||||||
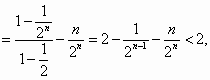 (13分)
(13分)