题目内容
已知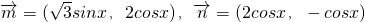
，函数
．
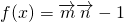（Ⅰ） 求函数f（x）的最小正周期和对称轴的方程；
（Ⅱ）设△ABC的角A，B，C的对边分别为a，b，c，且a=1，f（A）=0，求b+c的取值范围．
解：（Ⅰ）由题意可得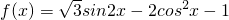
=
=
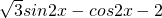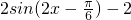．…（2分）
故f（x）的最小正周期为π，…（3分）
由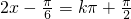
（k∈Z）得对称轴的方程为
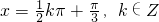．…（4分）
（Ⅱ）由f（A）=0得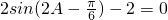
，即
，
∵
，∴
，∴
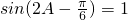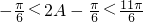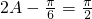，…（6分）
由正弦定理得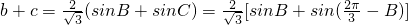
=
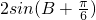…（8分）
∵，∴
，
∴
，
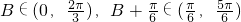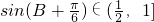∴b+c的取值范围为（1，2]．…（10分）
分析：（Ⅰ）由数量积的定义何三角函数的公式，可得函数为f（x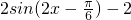）=，易得周期和对称轴；
（Ⅱ）由题意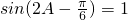可得，进而可得，由正弦定理可得b+c=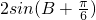，由B的范围可得sin（B+
）的范围，进而可得答案．
点评：本题考查向量数量积的运算，以及三角形的正弦定理，属中档题．
=
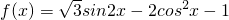
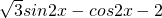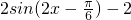=．…（2分）故f（x）的最小正周期为π，…（3分）
由
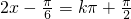（k∈Z）得对称轴的方程为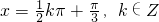．…（4分）（Ⅱ）由f（A）=0得
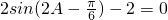，即，∵
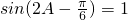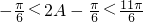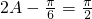，∴，∴，…（6分）由正弦定理得
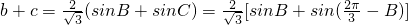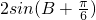=…（8分）∵
，∴，∴
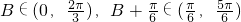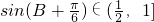，∴b+c的取值范围为（1，2]．…（10分）
分析：（Ⅰ）由数量积的定义何三角函数的公式，可得函数为f（x）=
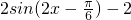，易得周期和对称轴；（Ⅱ）由题意可得
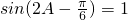，进而可得，由正弦定理可得b+c=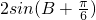，由B的范围可得sin（B+）的范围，进而可得答案．点评：本题考查向量数量积的运算，以及三角形的正弦定理，属中档题．
练习册系列答案
相关题目
（2012•钟祥市模拟）如图，已知幂函数y=xa的图象过点P（2，4），则图中阴影部分的面积等于（ ）