题目内容
已知椭圆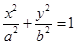 (
(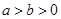 ),圆
),圆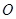 :
: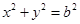 ,过椭圆上任一与顶点不重合的点
,过椭圆上任一与顶点不重合的点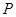 引圆
引圆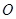 的两条切线,切点分别为
的两条切线,切点分别为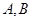 ,直线
,直线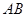 与
与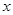 轴、
轴、 轴分别交于点
轴分别交于点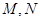 ,则
,则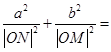
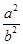
解析考点:椭圆的简单性质。
分析:设A(xA,yA ),B (xB,yB ),则可得切线PA、PB的方程,即可得到A,B 是xP?x+yP?y=b2 和圆x2+y2=b2 的交点,求出点M(b2/ xP,0),N(0,b2/ yP),从而得到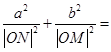 的值。
的值。
解答:
设A(xA,yA ),B (xB,yB ),则切线PA、PB的方程分别为 xA?x+yA?y=1,
xB?x+yB?y=b2.由于点P 是切线PA、PB的交点,
故点P的坐标满足切线PA的方程,也满足切线PAB的方程.
故A,B 是xP?x+yP?y=b2 和圆x2+y2=b2 的交点,
故点M(b2/ xP,0),N(0,b2/ yP),
又xP2 / a2+ yP2/ b2=1, = a2yP2/ b4+ a2xP2/ b4=(xP2 / a2+ yP2/ b2)?a2/ b2= a2/ b2。
∴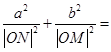
= a2yP2/ b4+ a2xP2/ b4=(xP2 / a2+ yP2/ b2)?a2/ b2= a2/ b2。
点评:本题考查椭圆的标准方程,以及简单性质的应用,得到故A,B 是xP?x+yP?y=b2 和圆x2+y2=b2 的交点,是解题的难点和关键。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽__________米.
时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽__________米. 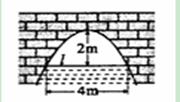
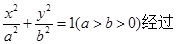 点
点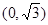 ,离心率为
,离心率为 ,左右焦点分别为
,左右焦点分别为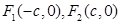
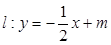 与椭圆交于
与椭圆交于 两点,与以
两点,与以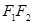 为直径的圆交于
为直径的圆交于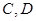 两点,且满足
两点,且满足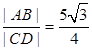 ,求直线
,求直线 的方程.
的方程.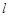 过抛物线
过抛物线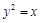 的焦点,且
的焦点,且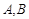 两点,若
两点,若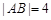 ,则弦
,则弦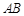 的中点到
的中点到 轴的距离为________
轴的距离为________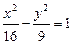 上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则| PQ |-| PR | 的最大值是 .
上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则| PQ |-| PR | 的最大值是 .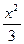 -
-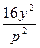 =1的左焦点在抛物线y2=2px的准线上,则p的值为______
=1的左焦点在抛物线y2=2px的准线上,则p的值为______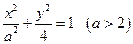 的离心率为
的离心率为
 ,则
,则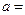 __________.
__________.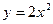 的焦点为
的焦点为 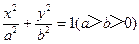 的左、右焦点分别是F1,F2,过F2作倾斜角为
的左、右焦点分别是F1,F2,过F2作倾斜角为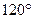 的直线与椭圆的一个交点为M,若MF1垂直于x轴,则椭圆的离心率为______
的直线与椭圆的一个交点为M,若MF1垂直于x轴,则椭圆的离心率为______