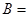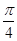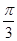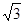题目内容
在△ABC中,内角A,B,C所对的边分别是a,b,c,已知a=2,c=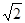 ,
,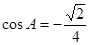 .
.
(1)求sinC和b的值;
(2)求cos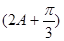 的值.
的值.
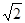 ,
,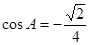 .
.(1)求sinC和b的值;
(2)求cos
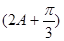 的值.
的值.(1)sinC=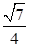 ,b=1;(2)
,b=1;(2)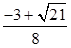 .
.
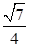 ,b=1;(2)
,b=1;(2)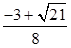 .
.试题分析:(1)△ABC中,利用同角三角函数的基本关系求出sinA,再由正弦定理求出sinC,再由余弦定理求得b=1;(2)利用二倍角公式求得cos2A的值,由此求得sin2A,再由两角和的余弦公式求出cos(2A+
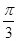 )=cos2Acos
)=cos2Acos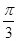 -sin2Asin
-sin2Asin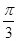 的值.
的值.解:(1)在△ABC中,由cosA=-
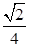 ,可得sinA=
,可得sinA=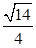 ,又由
,又由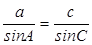 及a=2,c=
及a=2,c=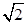 ,可得sinC=
,可得sinC=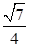 .
.由a2=b2+c2-2bccosA,得b2+b-2=0,
因为b>0,故解得b=1.所以sinC=
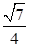 ,b=1 5分
,b=1 5分(2)由cosA=-
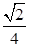 ,sinA=
,sinA=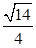 ,
,得cos2A=2cos2A-1=-
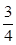 ,
,sin2A=2sinAcosA=-
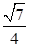 .
.所以,cos
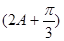 =cos2Acos
=cos2Acos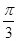 -sin2Asin
-sin2Asin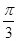 =
=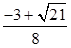 ..............10分
..............10分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
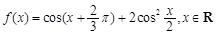 .
.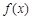 的值域;
的值域;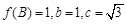 ,求a的值.
,求a的值.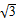 ,
,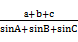 =________.
=________.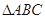 中,
中,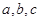 分别是三内角
分别是三内角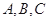 的对边,且
的对边,且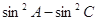 =
=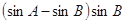 ,则角
,则角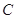 等于( )
等于( )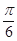
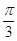
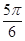
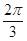
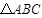 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为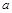 、
、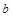 、
、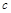 ,已知向量
,已知向量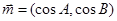 、
、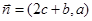 ,且
,且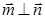 .
.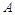 的大小;
的大小;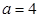 ,求
,求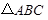 面积的最大值.
面积的最大值.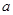 、
、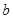 ,若2asinB=
,若2asinB=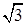 b,则角A等于________.
b,则角A等于________.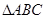 中,边
中,边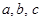 所对角分别为
所对角分别为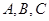 ,若
,若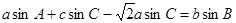 ,则
,则