题目内容
2.设a,b∈R,已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},0≤x<2}\\{lo{g}_{16}x,x≥2}\end{array}\right.$,若关于x的方程[f(x)]2+af(x)+b=0有且只有7个不同实数根,则$\frac{b}{a}$的取值范围是(-$\frac{3}{5}$,-$\frac{1}{2}$).分析 确定函数f(x)的性质,可得关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,则方程t2+at+b=0必有两个根t1,t2,其中t1=1,t2∈($\frac{1}{4}$,1),根据根与系数之间的关系,即可得出结论.
解答 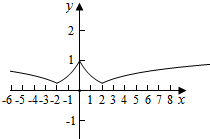 解:由题意,f(x)在(-∞,-2]和[0,2]上是减函数,在[-2,0]和[2,+∞)上是增函数,
解:由题意,f(x)在(-∞,-2]和[0,2]上是减函数,在[-2,0]和[2,+∞)上是增函数,
∴x=0时,函数取极大值1,x=±2时,取极小值$\frac{1}{4}$,
|x|≥16时,f(x)≥1,
∴关于x的方程[f(x)]2+a•f(x)+b=0(a、b∈R)有且只有7个不同实数根,
设t=f(x),
则方程t2+at+b=0必有两个根t1,t2,其中t1=1,t2∈($\frac{1}{4}$,1),
t1+t2=-a∈($\frac{5}{4}$,2),
则-2<a<-$\frac{5}{4}$,∴-$\frac{4}{5}$<$\frac{1}{a}$<-$\frac{1}{2}$
∵b=-a-1,
∴$\frac{3}{4}$<b<1,
∴$\frac{b}{a}$∈(-$\frac{3}{5}$,-$\frac{1}{2}$),
故答案为:(-$\frac{3}{5}$,-$\frac{1}{2}$).
点评 本题考查分段函数的应用,考查函数的性质,考查数形结合的数学思想,正确理解函数的性质是关键.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
10.0<a<1,函数$f(x)={log_a}({a^{2x}}-{a^x}-1)$,则f(x)>0的x取值范围是( )
| A. | (-∞,loga2) | B. | (loga2,+∞) | C. | (-∞,${log_a}\frac{{\sqrt{5}+1}}{2}$) | D. | (loga2,loga$\frac{{\sqrt{5}+1}}{2}$) |
17.当0<x≤$\frac{1}{2}$时,4x<logax,则实数a的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | $(0,\frac{{\sqrt{2}}}{2})$ | D. | $(\frac{{\sqrt{2}}}{2},1)$ |
14.已知p:x≥k,q:x2-x>2,如果p是q的充分不必要条件,则实数k的取值范围为( )
| A. | [1,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (-∞,-1] |
12. 如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).则区域M面积与矩形OABC面积之比为( )
如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).则区域M面积与矩形OABC面积之比为( )
 如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).则区域M面积与矩形OABC面积之比为( )
如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).则区域M面积与矩形OABC面积之比为( )| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |