题目内容
定义域为R的连续函数 ,对任意x都有
,对任意x都有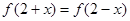 ,且其导函数
,且其导函数 满足
满足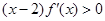 ,则当
,则当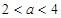 时,有( )
时,有( )
A. | B.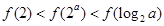 |
C.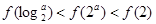 | D.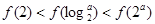 |
D
解析试题分析:∵对任意 都有
都有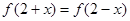 ,∴
,∴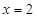 是
是 的对称轴,又∵
的对称轴,又∵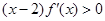 ,∴当
,∴当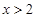 时,
时,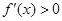 ,
, 是增函数;当
是增函数;当 时,
时,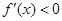 ,
, 是减函数;又∵
是减函数;又∵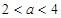 ,∴
,∴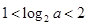 ,
,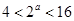 ;由
;由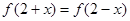 ,得
,得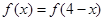 ,∴
,∴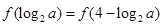 ,由
,由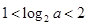 ,得
,得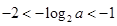 ,∴
,∴ ;∴
;∴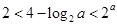 ,∴
,∴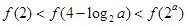 ,即
,即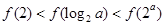 ,故选:D.
,故选:D.
考点:利用导数研究函数的单调性.

练习册系列答案
相关题目
若实数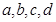 满足
满足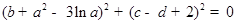 ,则
,则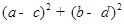 的最小值为( )
的最小值为( )
A.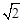 | B.2 | C.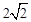 | D.8 |
若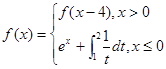 ,则f(2016)等于 ( )
,则f(2016)等于 ( )
| A.0 | B.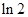 | C.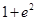 | D.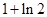 |
已知定义域为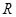 的函数
的函数 满足
满足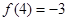 ,且对任意
,且对任意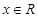 总有
总有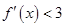 ,则不等式
,则不等式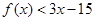 的解集为 ( )
的解集为 ( )
A.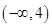 | B.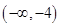 |
C.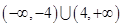 | D.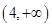 |
已知 为常数,函数
为常数,函数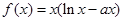 有两个极值点
有两个极值点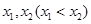 ,则( )
,则( )
A.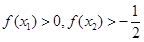 | B.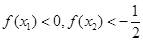 |
C.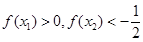 | D.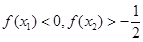 |
定积分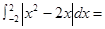 ( )
( )
| A.5 | B.6 | C.7 | D.8 |
已知函数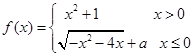 在点(1,2)处的切线与
在点(1,2)处的切线与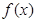 的图像有三个公共点,则
的图像有三个公共点,则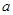 的取值范围是( )
的取值范围是( )
A.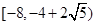 | B.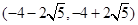 |
C.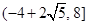 | D.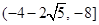 |
设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( ).
| A.?x∈R,f(x)≤f(x0) |
| B.-x0是f(-x)的极小值点 |
| C.-x0是-f(x)的极小值点 |
| D.-x0是-f(-x)的极小值点 |
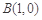 ,
,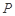 是函数
是函数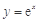 图象上不同于
图象上不同于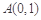 的一点.有如下结论:
的一点.有如下结论: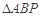 是等腰三角形;
是等腰三角形;