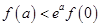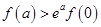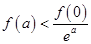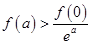题目内容
已知函数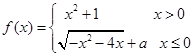 在点(1,2)处的切线与
在点(1,2)处的切线与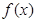 的图像有三个公共点,则
的图像有三个公共点,则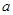 的取值范围是( )
的取值范围是( )
A.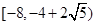 | B.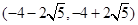 |
C.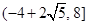 | D.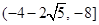 |
D
解析试题分析:当 时,
时, ,则
,则 ,则在点
,则在点 处的切线方程
处的切线方程 ;当
;当 时
时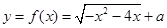 ,化简得
,化简得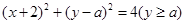 表示的是以
表示的是以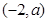 为圆心,
为圆心, 为半径的半圆.随着
为半径的半圆.随着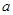 减小时,半圆向下移动,当半圆上一点
减小时,半圆向下移动,当半圆上一点 落在切线上是,切线
落在切线上是,切线 与
与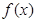 的图像有三个公共点,即
的图像有三个公共点,即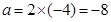 ;再向下移动,直到半圆与直线相切前,
;再向下移动,直到半圆与直线相切前,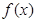 的图像有三个公共点,相切时与
的图像有三个公共点,相切时与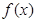 的图像有两个交点,即
的图像有两个交点,即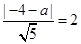 解得
解得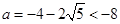 ,所以
,所以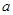 的取值范围为
的取值范围为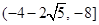 ,故选D.
,故选D.
考点:1.利用导数研究曲线上的切线方程;2.点到直线的距离与数形结合思想应用.

练习册系列答案
相关题目
定义域为R的连续函数 ,对任意x都有
,对任意x都有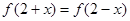 ,且其导函数
,且其导函数 满足
满足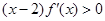 ,则当
,则当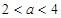 时,有( )
时,有( )
A. | B.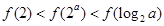 |
C.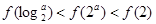 | D.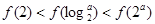 |
若曲线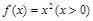 在点
在点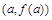 处的切线与两条坐标轴围成的三角形的面积为54,则
处的切线与两条坐标轴围成的三角形的面积为54,则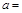 ( )
( )
| A.3 | B.6 | C.9 | D.18 |
设函数f(x)=x3-4x+a,0<a<2.若f(x)的三个零点为x1,x2,x3,且x1<x2<x3,则( )
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
不等式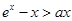 的解集为
的解集为 ,且
,且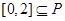 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A.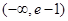 | B. | C.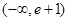 | D.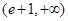 |
定义在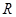 上的函数
上的函数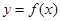 ,满足
,满足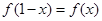 ,
,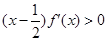 ,若
,若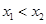 且
且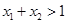 ,则有( )
,则有( )
A.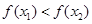 | B.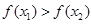 | C.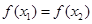 | D.不能确定 |
设函数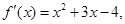 则
则 的单调减区间( )
的单调减区间( )
A.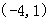 | B.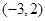 | C. | D.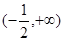 |
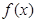 的图象上;②点A、B关于原点对称,则点(A,B)是函数
的图象上;②点A、B关于原点对称,则点(A,B)是函数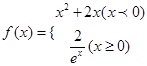 ,则
,则 是定义在R上的可导函数,且满足
是定义在R上的可导函数,且满足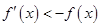 ,对于任意的正数
,对于任意的正数 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )