题目内容
点E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点,且BD=AC,则四边形EFGH是
菱形
菱形
.分析:作出如图的空间四边形,连接AC,BD可得一个三棱锥,将四个中点连接,得到一个四边形,可证明其是一个菱形.
解答: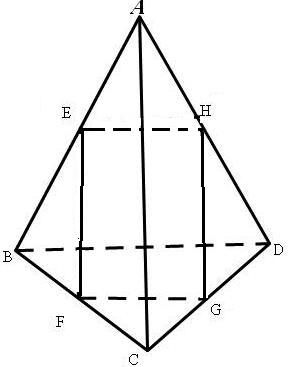 解:作出如图的空间四边形,
解:作出如图的空间四边形,
连接AC,BD可得一个三棱锥,
将四个中点连接,得到一个四边形EFGH,
由中位线的性质知,
EH∥FG,EF∥HG
故四边形EFGH是平行四边形,
又AC=BD,
故有HG=
AC=
BD=EH,
故四边形EFGH是菱形.
故答案为:菱形.
 解:作出如图的空间四边形,
解:作出如图的空间四边形,连接AC,BD可得一个三棱锥,
将四个中点连接,得到一个四边形EFGH,
由中位线的性质知,
EH∥FG,EF∥HG
故四边形EFGH是平行四边形,
又AC=BD,
故有HG=
| 1 |
| 2 |
| 1 |
| 2 |
故四边形EFGH是菱形.
故答案为:菱形.
点评:本题考查空间中直线与干线之间的位置关系,解题的关键是掌握空间中直线与直线之间位置关系的判断方法,本题涉及到线线平行的证明,中位线的性质等要注意这些知识在应用时的转化方式.

练习册系列答案
相关题目
点 E,F,G,H分别为空间四边形ABCD的边AB,BC,CD,AD的中点,则四边形EFGH是( )
| A、菱形 | B、梯形 | C、正方形 | D、平行四边形 |
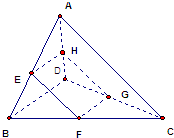 点E,F,G,H分别为空间四边形ABCD中AB,BC,CD,AD的中点,若AC=BD,且AC与BD成90°,则四边形EFGH是( )
点E,F,G,H分别为空间四边形ABCD中AB,BC,CD,AD的中点,若AC=BD,且AC与BD成90°,则四边形EFGH是( ) 如图三棱锥A-BCD中,截面四边形EFGH是梯形,其中EF∥GH,点E,F,G,H分别在AB、BC、CD、DA上;
如图三棱锥A-BCD中,截面四边形EFGH是梯形,其中EF∥GH,点E,F,G,H分别在AB、BC、CD、DA上;