Question

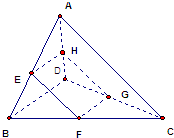点E，F，G，H分别为空间四边形ABCD中AB，BC，CD，AD的中点，若AC=BD，且AC与BD成90°，则四边形EFGH是（　　）

A．菱形

B．梯形

C．正方形

D．空间四边形

Answer 1

分析：先根据三角形的中位线定理整出两队对边平行且相等，是一个平行四边形，再证明四边形EFGH为菱形，然后说明∠EFG=90°，得到四边形是一个正方形．

解答：解：因为EH是△ABD的中位线，所以EH∥BD，且EH=

1

2

BD
同理FG∥BD，EF∥AC，且FG=

1

2

BD，EF=

1

2

AC．
所以EH∥FG，且EH=FG
∵AC=BD，
所以四边形EFGH为菱形．
∵AC与BD成90⁰
∴菱形是一个正方形，
故选C．

点评：本题考查简单几何体和公理四，本题解题的关键是要证明正方形常用方法是先证明它是菱形再证明一个角是直角，本题是一个基础题．