题目内容
已知函数 满足对任意实数
满足对任意实数 都有
都有 成立,且当
成立,且当 时,
时, ,
, .
.
(1)求 的值;
的值;
(2)判断 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数 ,总能找到一个正实数
,总能找到一个正实数 ,使得当
,使得当 时,
时, ,则称函数
,则称函数 在
在 处连续。试证明:
处连续。试证明: 在
在 处连续.
处连续.
【答案】
(1)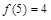 ;(2)
;(2)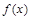 在
在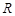 上单调递增; (3)详见试题解析.
上单调递增; (3)详见试题解析.
【解析】
试题分析:(1)利用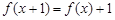 求
求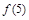 ,可得
,可得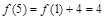 ;(2)利用函数单调性的定义:设
;(2)利用函数单调性的定义:设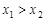 ,则
,则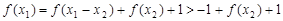 ,
,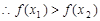 ,从而
,从而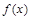 在
在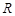 上单调递增; (3)利用赋值法先求
上单调递增; (3)利用赋值法先求 .要证
.要证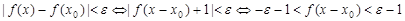 ,对
,对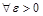 ,当
,当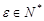 时,取
时,取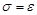 ,则当
,则当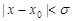 ,即
,即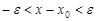 时,由
时,由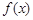 单增可得
单增可得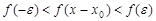 ,即
,即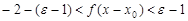 ;当
;当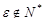 时,必
时,必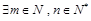 ,使得
,使得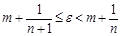 ,取
,取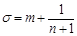 ,利用
,利用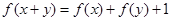 证明.
证明.
试题解析:(1)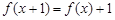
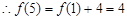 ;
;
(2)设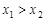 ,则
,则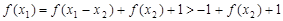 ,
,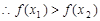 ,
,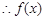 在
在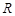 上单调递增;
上单调递增;
(3)令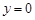 ,得
,得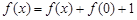 ,
,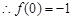 .对任意
.对任意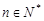 ,
,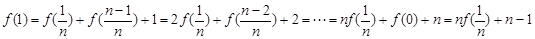 ,
,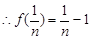 ,
,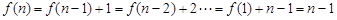 ,又
,又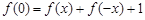 ,
,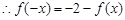 ,要证
,要证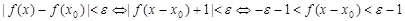 ,对
,对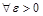 ,当
,当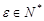 时,取
时,取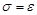 ,则当
,则当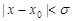 ,即
,即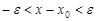 时,由
时,由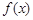 单增可得
单增可得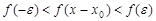 ,即
,即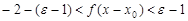 ;当
;当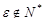 时,必
时,必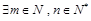 ,使得
,使得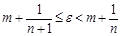 ,取
,取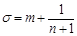 ,则当
,则当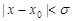 ,即
,即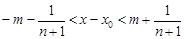 时,有
时,有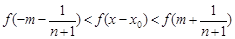 ,而
,而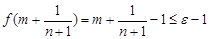 ,
,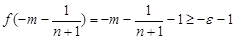 ,
,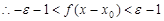 .
.
综上,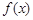 在
在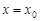 处连续.
处连续.
考点:1.赋值法求抽象函数的函数值;2.抽血函数的单调性;3.抽象函数的连续性.

练习册系列答案
相关题目