题目内容
10.若双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,则双曲线M的离心率的取值范围是$(\sqrt{2},+∞)$.分析 双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,可得$\frac{b}{a}$>1,利用e=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,可求双曲线M的离心率的取值范围.
解答 解:∵双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,
∴$\frac{b}{a}$>1,
∴e=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$>$\sqrt{2}$,
即e∈$(\sqrt{2},+∞)$.
故答案为:$(\sqrt{2},+∞)$.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
20.若(x2-1)+(x2+3x+2)i是纯虚数,则实数x的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 以上都不对 |
1.积分$\int_0^4xdx$的值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
18.△ABC中,角A,B,C所对的边分别为a,b,c,若a=$\sqrt{7}$,b=3,c=2,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
2.现有5名同学去听同时进行的3个课外知识讲座,每名同学可自由选择其中的一个讲座,不同选法的种数是( )
| A. | C${\;}_{5}^{2}$ | B. | A${\;}_{5}^{2}$ | C. | 35 | D. | 52 |
19.已知随机变量ξ:B(10,0.04),随机变量ξ的数学期望E(ξ)=( )
| A. | 0.2 | B. | 0.4 | C. | 2 | D. | 4 |
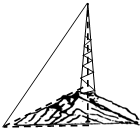 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上