题目内容
圆x2+(y+1)2=1的圆心坐标是 ,如果直线x+y+a=0与该圆有公共点,那么实数a的取值范围是 .
考点:直线与圆相交的性质,圆的标准方程
专题:直线与圆
分析:根据圆的标准方程求得圆的圆心坐标,再根据圆心到直线的距离小于或等于半径,求得a的范围.
解答:
解:圆x2+(y+1)2=1的圆心坐标是(0,-1),
如果直线x+y+a=0与该圆有公共点,那么圆心到直线的距离小于或等于半径,
即
≤1,求得1-
≤a≤1+
,故实数a的取值范围是[1-
,1+
],
故答案为:[1-
,1+
].
如果直线x+y+a=0与该圆有公共点,那么圆心到直线的距离小于或等于半径,
即
| |0-1+a| | ||
|
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:[1-
| 2 |
| 2 |
点评:本题主要考查圆的标准方程,直线和圆相交的性质,点到直线的距离公式,属于基础题.

练习册系列答案
相关题目
一个命题与他们的逆命题、否命题、逆否命题这4个命题中( )
| A、真命题与假命题的个数相同 |
| B、真命题的个数一定是奇数 |
| C、真命题的个数一定是偶数 |
| D、真命题的个数可能是奇数,也可能是偶数 |
如下图①对应于函数f(x),则在下列给出的四个函数中,图②对应的函数只能是( )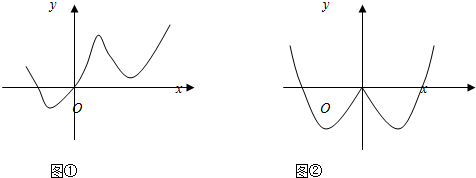

| A、y=f(|x|) |
| B、y=|f(x)| |
| C、y=f(-|x|) |
| D、y=-f(|x|) |
已知等比数列{an}的首项为a1,公比为q,且有
(
-qn)=
,则首项a1的取值范围是( )
| lim |
| n→∞ |
| a1 |
| 1+q |
| 1 |
| 2 |
A、0<a1<1且a1≠
| ||
| B、0<a1<3且a1=-3 | ||
C、0<a1<
| ||
D、0<a1<1且a1≠
|