题目内容
设关于x的一元二次方程x2+2ax+b2=0.
(1)若a,b是从区间[0,3]任取的两个整数,求上述方程有实根的概率;
(2)若a,b是从区间[0,3]上任取的两个实数,求上述方程有实根的概率.
(1)若a,b是从区间[0,3]任取的两个整数,求上述方程有实根的概率;
(2)若a,b是从区间[0,3]上任取的两个实数,求上述方程有实根的概率.
考点:几何概型,二次函数的性质
专题:概率与统计
分析:(1)由一元二次方程的判别式大于等于0得到方程x2+2ax+b2=0有实数根的充要条件为a≥b,用列举法求出a,b是从[0,3]任取的两个整数即从0,1,2,3四个数中任取的两个数,查出满足a≥b的事件数,然后直接利用古典概型概率计算公式求解;
(2)由题意求出点(a,b)所构成的正方形的面积,再由线性规划知识求出满足a≥b的区域面积,由测度比是面积比求概率.
(2)由题意求出点(a,b)所构成的正方形的面积,再由线性规划知识求出满足a≥b的区域面积,由测度比是面积比求概率.
解答:
解:设事件A为“方程x2+2ax+b2=0有实数根”.
当a≥0,b≥0时,方程x2+2ax+b2=0有实数根的充要条件为a≥b
(1)基本事件共16个:(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),
(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3).其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含10个基本事件.
事件A发生的概率为P(A)=
;
(2)试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤3}.
构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤3,a≥b}.
如图,
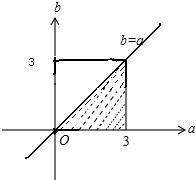
∴所求的概率P(A)=
=
.
当a≥0,b≥0时,方程x2+2ax+b2=0有实数根的充要条件为a≥b
(1)基本事件共16个:(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),
(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3).其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含10个基本事件.
事件A发生的概率为P(A)=
| 9 |
| 16 |
(2)试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤3}.
构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤3,a≥b}.
如图,

∴所求的概率P(A)=
| ||
| 3×3 |
| 1 |
| 2 |
点评:本题考查了古典概型及其概率计算公式,考查了几何概型的概率,关键是理解(2)的测度比,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果l1、l2两直线的斜率是方程x2-4x+1=0的两实根,那么l1,l2的夹角是( )
| A、60° | B、45° |
| C、30° | D、90° |
将容量为100的样本数据,按从大到小的顺序分成8个组,如表:
则第6组的频率为( )
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 | 11 | 14 | 12 | 13 | 13 | x | 12 | 10 |
| A、0.14 | B、14 |
| C、0.15 | D、15 |
△ABC中,内角∠B=45°,角C的对边c=2
,角B的对边b=
,则角A等于( )
| 2 |
4
| ||
| 3 |
| A、15° | B、75° |
| C、105° | D、15°或75° |