题目内容
已知等比数列{an}的首项为a1,公比为q,且有
(
-qn)=
,则首项a1的取值范围是( )
| lim |
| n→∞ |
| a1 |
| 1+q |
| 1 |
| 2 |
A、0<a1<1且a1≠
| ||
| B、0<a1<3且a1=-3 | ||
C、0<a1<
| ||
D、0<a1<1且a1≠
|
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:对q讨论,①q=1时,②|q|<1时,分别求出极限,解方程或不等式,即可得到范围.
解答:
解:①q=1时,
-1=
,解得,a1=3;
②|q|<1时,且q≠0,
=
,则a1=
(1+q),
又0<1+q<1或1<1+q<2
则有0<a1<
或
<a1<1.
故选D.
| a1 |
| 2 |
| 1 |
| 2 |
②|q|<1时,且q≠0,
| a1 |
| 1+q |
| 1 |
| 2 |
| 1 |
| 2 |
又0<1+q<1或1<1+q<2
则有0<a1<
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查数列的极限运算,注意讨论公比,考查运算能力,属于中档题和易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
目标函数z=2x+y,变量x,y满足
,则有( )
|
| A、zmax=12,zmin=3 | ||
B、zmax=10,zmin=
| ||
| C、zmin=3,z无最大值 | ||
| D、z既无最大值,也无最小值 |
在等差数列{an}中,a5=33,公差d=3,则201是该数列的第( )项.
| A、60 | B、61 | C、62 | D、63 |
| ∫ |
-
|
| A、0 | B、1 | C、2 | D、π |
△ABC中,内角∠B=45°,角C的对边c=2
,角B的对边b=
,则角A等于( )
| 2 |
4
| ||
| 3 |
| A、15° | B、75° |
| C、105° | D、15°或75° |
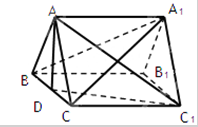 如图所示,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为3,且侧棱AA1⊥面ABC,点D是BC的中点,求证:平面BB1C1C丄平面ADC1.
如图所示,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为3,且侧棱AA1⊥面ABC,点D是BC的中点,求证:平面BB1C1C丄平面ADC1.