题目内容
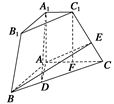
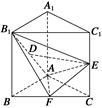
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,
∠BAC=90°,A1A⊥平面ABC,A1A= ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, =
= .
.
(1)证明:平面A1AD⊥平面BCC1B1;
(2)求二面角A—CC1—B的余弦值.
∠BAC=90°,A1A⊥平面ABC,A1A=
 ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, =
= .
.(1)证明:平面A1AD⊥平面BCC1B1;
(2)求二面角A—CC1—B的余弦值.

(1) 证明略(2) 二面角A—CC1—B余弦值为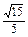 .
.
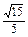 .
.方法一 (1) ∵A1A⊥平面ABC,BC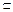 平面ABC,
平面ABC,
∴A1A⊥BC.
在Rt△ABC中,AB= ,AC=2,∴BC=
,AC=2,∴BC=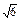 .
.
∵BD∶DC=1∶2,∴BD=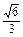 .又
.又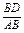 =
=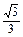 =
=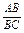 ,
,
∴△DBA∽△ABC,∴∠ADB=∠BAC=90°,
即AD⊥BC.
又A1A∩AD=A,∴BC⊥平面A1AD.
∵BC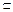 平面BCC1B1,∴平面A1AD⊥平面BCC1B1.
平面BCC1B1,∴平面A1AD⊥平面BCC1B1.
(2) 如图①,作AE⊥C1C交C1C于E点,连接BE,由已知得AB⊥平面ACC1A1,
∴AE是BE在平面ACC1A1内的射影.
由三垂线定理知BE⊥CC1,
∴∠AEB为二面角A—CC1—B的平面角. 图①
过C1作C1F⊥AC交AC于F点,
则CF=AC-AF=1,
C1F=A1A= ,∴∠C1CF=60°.
,∴∠C1CF=60°.
在Rt△AEC中,
AE=ACsin60°=2×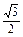 =
= ,
,
在Rt△BAE中,tan∠AEB=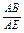 =
=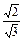 =
=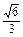 ,
,
∴cos∠AEB=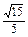 ,
,
即二面角A—CC1—B余弦值为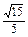 .
.
方法二 (1) 如图②,建立空间直角坐标系,
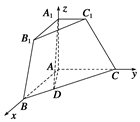
图②
则A(0,0,0),B( ,0,0),C(0,2,0),
,0,0),C(0,2,0),
A1(0,0, ),C1(0,1,
),C1(0,1,  ).
).
∵BD∶DC=1∶2,∴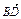 =
=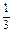
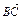 ,
,
∴D点坐标为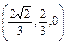 ,
,
∴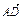 =
=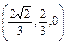 ,
,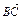 =(-
=(- ,2,0),
,2,0),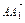 =(0,0,
=(0,0, ).
).
∵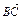 ·
·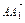 =0,
=0,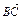 ·
·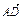 =0,
=0,
∴BC⊥AA1,BC⊥AD.又A1A∩AD=A,
∴BC⊥平面A1AD.又BC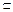 平面BCC1B1,
平面BCC1B1,
∴平面A1AD⊥平面BCC1B1.
(2) ∵BA⊥平面ACC1A1,取m=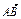 =(
=( ,0,0)为平面ACC1A1的法向量.
,0,0)为平面ACC1A1的法向量.
设平面BCC1B1的法向量为n=(x,y,z),
则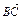 ·n=0,
·n=0,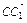 ·n=0,
·n=0,
∴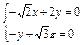
∴x= y,z=
y,z=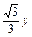 ,可取y=1,则n=
,可取y=1,则n=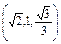 ,
,
cos〈m,n〉=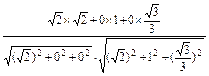
=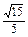 ,
,
即二面角A—CC1—B的余弦值为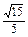 .
.
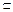 平面ABC,
平面ABC,
∴A1A⊥BC.
在Rt△ABC中,AB=
 ,AC=2,∴BC=
,AC=2,∴BC=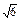 .
.∵BD∶DC=1∶2,∴BD=
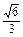 .又
.又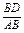 =
=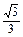 =
=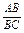 ,
,∴△DBA∽△ABC,∴∠ADB=∠BAC=90°,
即AD⊥BC.
又A1A∩AD=A,∴BC⊥平面A1AD.
∵BC
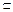 平面BCC1B1,∴平面A1AD⊥平面BCC1B1.
平面BCC1B1,∴平面A1AD⊥平面BCC1B1.(2) 如图①,作AE⊥C1C交C1C于E点,连接BE,由已知得AB⊥平面ACC1A1,
∴AE是BE在平面ACC1A1内的射影.
由三垂线定理知BE⊥CC1,
∴∠AEB为二面角A—CC1—B的平面角. 图①
过C1作C1F⊥AC交AC于F点,
则CF=AC-AF=1,
C1F=A1A=
 ,∴∠C1CF=60°.
,∴∠C1CF=60°.在Rt△AEC中,
AE=ACsin60°=2×
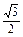 =
= ,
,在Rt△BAE中,tan∠AEB=
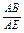 =
=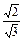 =
=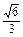 ,
,∴cos∠AEB=
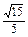 ,
,即二面角A—CC1—B余弦值为
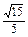 .
.方法二 (1) 如图②,建立空间直角坐标系,

图②
则A(0,0,0),B(
 ,0,0),C(0,2,0),
,0,0),C(0,2,0),A1(0,0,
 ),C1(0,1,
),C1(0,1,  ).
).∵BD∶DC=1∶2,∴
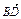 =
=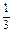
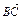 ,
,∴D点坐标为
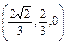 ,
,∴
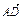 =
=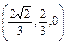 ,
,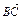 =(-
=(- ,2,0),
,2,0),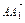 =(0,0,
=(0,0, ).
).∵
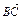 ·
·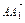 =0,
=0,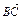 ·
·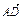 =0,
=0,∴BC⊥AA1,BC⊥AD.又A1A∩AD=A,
∴BC⊥平面A1AD.又BC
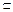 平面BCC1B1,
平面BCC1B1,∴平面A1AD⊥平面BCC1B1.
(2) ∵BA⊥平面ACC1A1,取m=
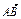 =(
=( ,0,0)为平面ACC1A1的法向量.
,0,0)为平面ACC1A1的法向量.设平面BCC1B1的法向量为n=(x,y,z),
则
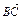 ·n=0,
·n=0,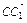 ·n=0,
·n=0,∴
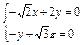
∴x=
 y,z=
y,z=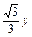 ,可取y=1,则n=
,可取y=1,则n=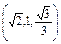 ,
,cos〈m,n〉=
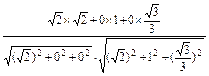
=
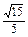 ,
,即二面角A—CC1—B的余弦值为
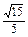 .
.
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目

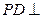 底面ABCD,PD=DC,E是PC的中点,作
底面ABCD,PD=DC,E是PC的中点,作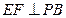 交PB于F.
交PB于F.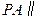 平面EDB;
平面EDB;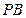
 平面EFD.
平面EFD.

 ,BC=
,BC= ,则P-ABC的体积V的取值范围是_____________。
,则P-ABC的体积V的取值范围是_____________。