题目内容
如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB,PB的中点.

(I)求证:EF⊥CD;
(II)求DB与平面DEF所成角的正弦值;
(III)在平面PAD内是否存在一点G,使G在平面PCB上的射影为△PCB的外心,若存在,试确定点G的位置;若不存在,说明理由.

(I)求证:EF⊥CD;
(II)求DB与平面DEF所成角的正弦值;
(III)在平面PAD内是否存在一点G,使G在平面PCB上的射影为△PCB的外心,若存在,试确定点G的位置;若不存在,说明理由.
(2)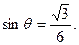 (3)中点
(3)中点
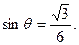 (3)中点
(3)中点以DA,DC,DP所在直线分别为x轴,y轴,z轴建立空间直角坐标系(如图).
、
设AD=a,则D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),E(a,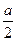 ,0),
,0),
P(0,0,a),F(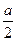 ,
,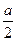 ,
,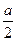 ).
).
(I)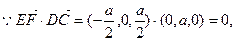
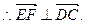
(II)设平面DEF的法向量为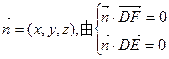
得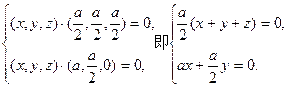
取x=1,则y=-2,z=1.
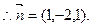
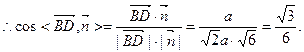
设DB与平面DEF所成角为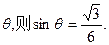
(III)假设存在点G满足题意
因为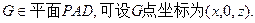
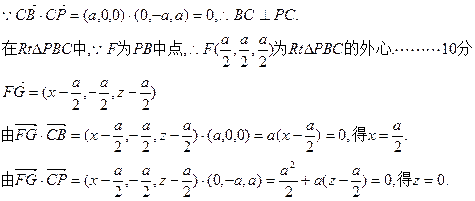
∴存在点G,其坐标为(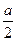 ,0,0),即G点为AD的中点
,0,0),即G点为AD的中点

、
设AD=a,则D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),E(a,
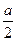 ,0),
,0),P(0,0,a),F(
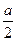 ,
,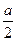 ,
,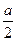 ).
).(I)
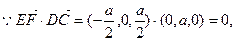
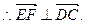
(II)设平面DEF的法向量为
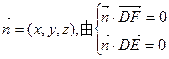
得
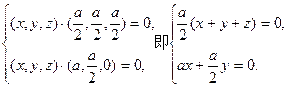
取x=1,则y=-2,z=1.
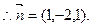
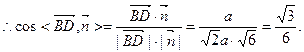
设DB与平面DEF所成角为
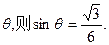
(III)假设存在点G满足题意
因为
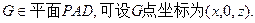
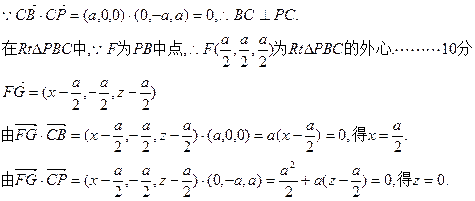
∴存在点G,其坐标为(
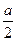 ,0,0),即G点为AD的中点
,0,0),即G点为AD的中点
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 中,
中, ,
,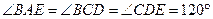 .
.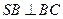 ;
;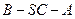 的大小.
的大小.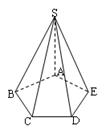
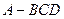 中,
中,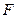 是
是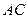 上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H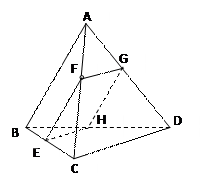
 中,
中,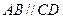 ,
,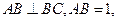
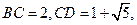 过
过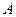 作
作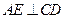 ,垂足为
,垂足为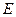 ,
,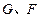 分别为
分别为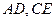 的中点,现将
的中点,现将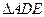 沿
沿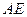 折叠使二面角
折叠使二面角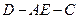 的平面角的正切值为
的平面角的正切值为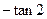 .
.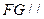 平面
平面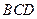 ;
;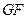 与
与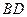 所成的角的余弦值;
所成的角的余弦值;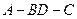 的大小.
的大小.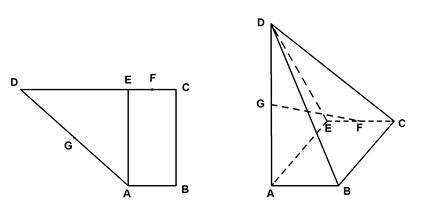
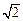 ,BB1=3,D为A1C1的中点,F在线段AA1上.
,BB1=3,D为A1C1的中点,F在线段AA1上.
 8.
8. cm
cm
 cm
cm
 ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, =
= .
.