题目内容
定义在R上的偶函数f(x)在[0,+∞)上是增函数,且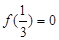 ,则不等式
,则不等式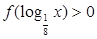 的解集是( )
的解集是( )
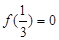 ,则不等式
,则不等式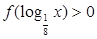 的解集是( )
的解集是( )A.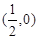 | B.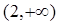 | C.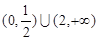 | D.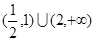 |
C
分析:先利用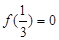 ,不等式
,不等式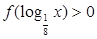 可化为f(|log
可化为f(|log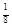 x|)>f(
x|)>f(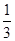 ),根据R上的偶函数f(x)在[0,+∞)上是增函数
),根据R上的偶函数f(x)在[0,+∞)上是增函数
,即可求出不等式的解集.
解答:解:由题意,不等式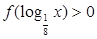 可化为f(|
可化为f(|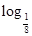 x|)>f(
x|)>f(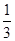 )
)
∵R上的偶函数f(x)在[0,+∞)上是增函数
∴|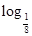 x|>
x|>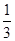
∴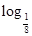 x>
x>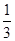
或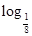 x<-
x<-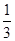
∴0<x<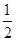 或x>2
或x>2
∴不等式f(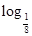 x)>0的解集是(0,
x)>0的解集是(0,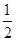 )∪(2,+∞)
)∪(2,+∞)
故选C.
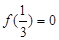 ,不等式
,不等式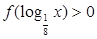 可化为f(|log
可化为f(|log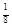 x|)>f(
x|)>f(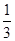 ),根据R上的偶函数f(x)在[0,+∞)上是增函数
),根据R上的偶函数f(x)在[0,+∞)上是增函数,即可求出不等式的解集.
解答:解:由题意,不等式
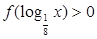 可化为f(|
可化为f(|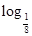 x|)>f(
x|)>f(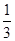 )
)∵R上的偶函数f(x)在[0,+∞)上是增函数
∴|
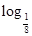 x|>
x|>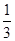
∴
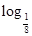 x>
x>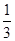
或
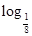 x<-
x<-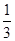
∴0<x<
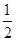 或x>2
或x>2∴不等式f(
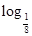 x)>0的解集是(0,
x)>0的解集是(0,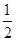 )∪(2,+∞)
)∪(2,+∞)故选C.

练习册系列答案
相关题目
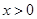 时,
时,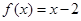 ,那么不等式
,那么不等式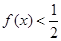 的解集是 ( )
的解集是 ( )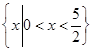
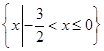
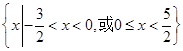
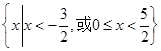
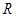 上的偶函数
上的偶函数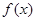 满足
满足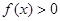 ,
,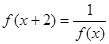 对任意
对任意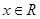 恒成立,则
恒成立,则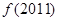 等于( )
等于( )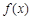 的图像关于点
的图像关于点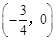 对称,且满足
对称,且满足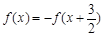 ,
,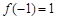 ,
,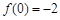 ,则
,则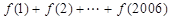 的值为
的值为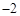

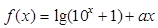 是偶函数,
是偶函数,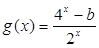 是奇函数,那么
是奇函数,那么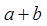 的值为( )
的值为( )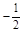
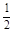
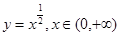
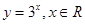
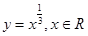
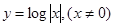
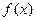 是定义在实数有R上的奇函数,若x≥0时,
是定义在实数有R上的奇函数,若x≥0时,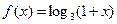 ,则
,则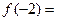 ___ __.
___ __.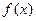 是连续的偶函数,且当
是连续的偶函数,且当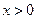 时
时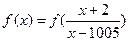 的所有
的所有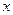 之和为
之和为