题目内容
 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
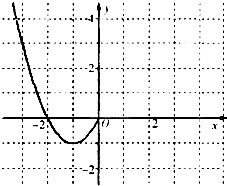
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域;
(3)若方程f(x)-m=0有四个解,求m的范围.
分析:(1)根据函数f(x)是定义在R上的偶函数,图象关于y轴对称,从而得到函数f(x)在y轴右侧的图象,再根据图象得到增区间;
(2)根据函数图象可得函数的解析式,和值域;
(3)要求方程f(x)-m=0有四个解,只需y=f(x)与y=m有四个个交点,结合图象可得m的取值范围.
(2)根据函数图象可得函数的解析式,和值域;
(3)要求方程f(x)-m=0有四个解,只需y=f(x)与y=m有四个个交点,结合图象可得m的取值范围.
解答:解;(1)函数图象如右图所示:
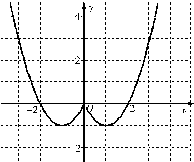
f(x)的递增区间是(-1,0),(1,+∞).
(2)根据图象可知解析式为:f(x)=
,值域为:{y|y≥-1}.
(3)根据图象可知-1<m<0时y=f(x)与y=m有四个个交点
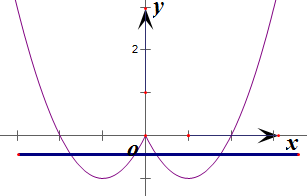
∴方程f(x)-m=0有四个解,m的范围是:-1<m<0.

f(x)的递增区间是(-1,0),(1,+∞).
(2)根据图象可知解析式为:f(x)=
|
(3)根据图象可知-1<m<0时y=f(x)与y=m有四个个交点

∴方程f(x)-m=0有四个解,m的范围是:-1<m<0.
点评:本题主要考查了偶函数的图象,以及函数单调性和值域,考查画图能力,属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+