题目内容
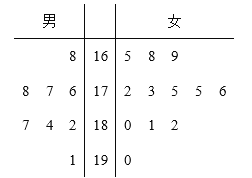
【题目】第30届夏季奥运会将于2012年7月27日在伦敦举行,当地某学校招募了8名男志愿者和12名女志愿者.将这20名志愿者的身高编成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(I)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析,
;(Ⅱ)见解析,![]() .
.
【解析】
(Ⅰ)由茎叶图读出“高个子”和“非高个子”的人数,然后得出分层抽样样本中相应的人数,然后先计算“没有一名“高个子”被选中”的概率,从而可得出“至少有一名“高个子”被选中”的概率;(Ⅱ)依题意,所选志愿者中能担任“礼仪小姐”的人数X的取值分别为![]() ,分别计算其概率,列出表格,求出期望即可.
,分别计算其概率,列出表格,求出期望即可.
解:(Ⅰ)根据茎叶图,有“高个子”8人,“非高个子”12人,
用分层抽样的方法,每个人被抽中的概率是![]() ,
,
所以选中的“高个子”有![]() 人,“非高个子”有
人,“非高个子”有![]() 人
人
用事件![]() 表示“至少有一名“高个子”被选中”,
表示“至少有一名“高个子”被选中”,
则它的对立事件![]() 表示“没有一名“高个子”被选中”,
表示“没有一名“高个子”被选中”,
则![]()
因此,至少有一人是“高个子”的概率是![]()
(Ⅱ)依题意,所选志愿者中能担任“礼仪小姐”的人数X的取值分别为![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
因此,X的分布列如下:
X | 0 | 1 | 2 | 3 |
|
|
|
|
|
所以X的数学期望![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目