题目内容
已知数列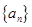 、
、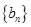 满足:
满足: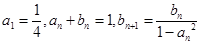 .
.
(1)求 ;
;
(2) 证明数列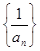 为等差数列,并求数列
为等差数列,并求数列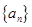 和
和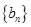 的通项公式;
的通项公式;
(3)设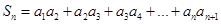 ,求实数
,求实数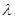 为何值时
为何值时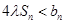 恒成立。
恒成立。
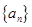 、
、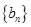 满足:
满足: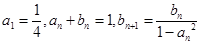 .
.(1)求
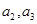 ;
;(2) 证明数列
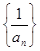 为等差数列,并求数列
为等差数列,并求数列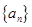 和
和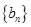 的通项公式;
的通项公式;(3)设
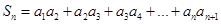 ,求实数
,求实数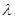 为何值时
为何值时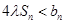 恒成立。
恒成立。(1) 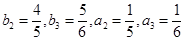 ;
;
(2)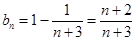 ;
;
(3)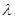 ≤1时,
≤1时,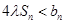 恒成立 。
恒成立 。
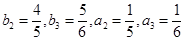 ;
;(2)
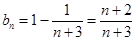 ;
;(3)
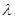 ≤1时,
≤1时,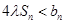 恒成立 。
恒成立 。试题分析:(1) ∵
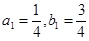 ∴
∴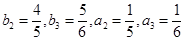 . 4分
. 4分(2)∵
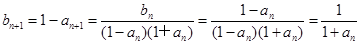
∴
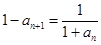 ,
,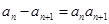
∴
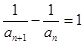
∴数列{
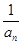 }是以4为首项,1为公差的等差数列 6分
}是以4为首项,1为公差的等差数列 6分∴
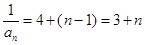
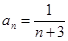 ∴
∴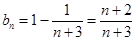 8分
8分(3)
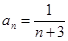
∴
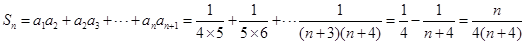
∴
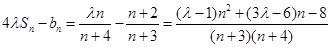 10分
10分由条件可知
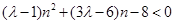 恒成立即可满足条件
恒成立即可满足条件设
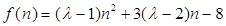
当
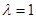 时,
时,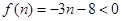 恒成立,
恒成立,当
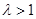 时,由二次函数的性质知不可能成立
时,由二次函数的性质知不可能成立当
 时,对称轴
时,对称轴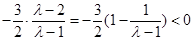 12分
12分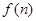 在
在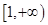 为单调递减函数.
为单调递减函数. 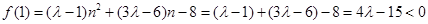
∴
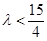 ∴
∴ 时
时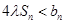 恒成立 13分
恒成立 13分综上知:
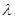 ≤1时,
≤1时,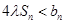 恒成立 14分
恒成立 14分点评:难题,本题综合性较强,综合考查数列的递推公式,等差数列的通项公式,裂项相消法,数列不等式的证明。确定等差数列的通项公式,往往利用已知条件,建立相关元素的方程组,以达到解题目的。本题从递推公式出发,研究“倒数数列”的特征,达到解题目的。涉及数列和的不等式证明问题,往往先求和、再放缩、得证明。本题通过构造函数、研究函数的最值,达到证明目的。

练习册系列答案
相关题目
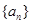 为等比数列, 其前
为等比数列, 其前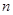 项和为
项和为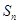 , 已知
, 已知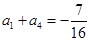 , 且对于任意的
, 且对于任意的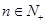 有
有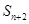 ,
, 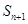 成等差;求数列
成等差;求数列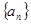 中,
中,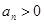 ,
,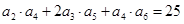 ,那么
,那么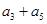 等于
等于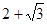 与
与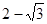 的等比中项为________________。
的等比中项为________________。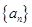 是公比为正数的等比数列,若
是公比为正数的等比数列,若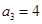 ,
,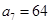 ,则
,则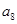 =( )
=( )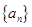 的前n项和为
的前n项和为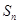 ,若
,若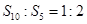 ,则
,则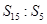 的值为
的值为 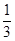
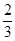
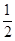
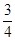
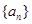 的各项均为正数,
的各项均为正数,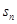 为其前
为其前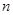 项和,对于任意的
项和,对于任意的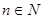 ,满足关系式
,满足关系式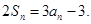
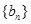 的通项公式是
的通项公式是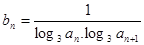 ,前
,前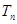 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有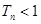
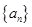 中,已知
中,已知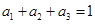 ,
,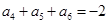 ,则该数列的前15项的和
,则该数列的前15项的和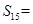 __ __.
__ __.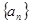 的首项为
的首项为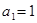 ,其前
,其前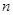 项和为
项和为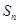 ,且对任意正整数
,且对任意正整数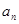 、
、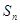 成等差数列.
成等差数列.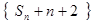 成等比数列;
成等比数列;