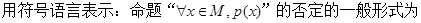题目内容
设命题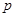 :函数
:函数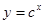 在
在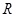 上单调递减,命题
上单调递减,命题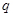 :不等式
:不等式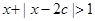 的解集为
的解集为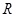 ,若
,若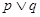 为真,
为真,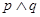 为假,求实数
为假,求实数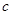 的取值范围.
的取值范围.
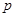 :函数
:函数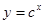 在
在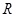 上单调递减,命题
上单调递减,命题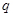 :不等式
:不等式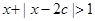 的解集为
的解集为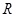 ,若
,若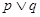 为真,
为真,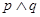 为假,求实数
为假,求实数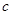 的取值范围.
的取值范围.由函数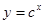 在R上单调递减知0<c<1,所以命题p为真命题时c的取值范围是0<c<1,令y=x+|x-2c|,则
在R上单调递减知0<c<1,所以命题p为真命题时c的取值范围是0<c<1,令y=x+|x-2c|,则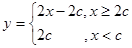 .
.
不等式x+|x-2a|>1的解集为R,只要ymin>1即可,而函数y在R上的最小值为2c,
所以2c>1,即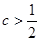 .
.
⑴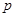 真
真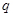 假
假 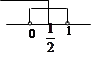 则
则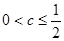
⑵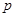 假
假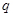 真
真 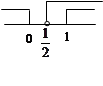 则
则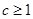
综上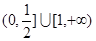 .
.
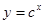 在R上单调递减知0<c<1,所以命题p为真命题时c的取值范围是0<c<1,令y=x+|x-2c|,则
在R上单调递减知0<c<1,所以命题p为真命题时c的取值范围是0<c<1,令y=x+|x-2c|,则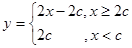 .
.不等式x+|x-2a|>1的解集为R,只要ymin>1即可,而函数y在R上的最小值为2c,
所以2c>1,即
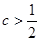 .
.⑴
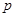 真
真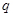 假
假 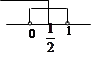 则
则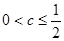
⑵
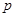 假
假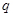 真
真 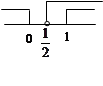 则
则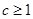
综上
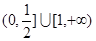 .
.先通过指数函数的单调性求出p为真命题的c的范围,再通过构造函数求绝对值函数的最值进一步求出命题q为真命题的c的范围,分p真q假与p假q真两类求出c的范围即可.

练习册系列答案
相关题目
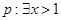 ,
,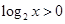 ,则
,则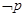 为 .
为 . 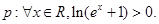 则
则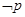 为
为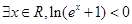
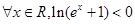
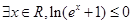
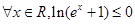
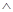 q为假,p
q为假,p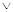 q为真,求m的取值范围.
q为真,求m的取值范围.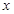 的不等式
的不等式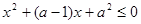 的解集为
的解集为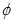 ;
;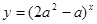 为增函数.
为增函数.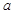 的取值范围.
的取值范围.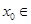 R,
R,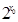
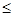 0”的否定是( ).
0”的否定是( ). 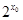 >0
>0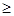 0
0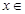 R,
R, 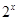
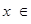 R,
R, 
 ,
,