题目内容
已知动圆 与圆
与圆 和圆
和圆 都外切,则动圆圆心
都外切,则动圆圆心 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 | C.双曲线 | D.双曲线的一支 |
D
解析试题分析:设动圆 的圆心坐标为(x,y),半径为
的圆心坐标为(x,y),半径为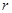 ,由于动圆
,由于动圆 与圆
与圆 和圆
和圆 都外切,所以
都外切,所以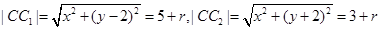 ,所以
,所以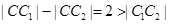 ,根据双曲线的定义可知动圆
,根据双曲线的定义可知动圆 的轨迹为双曲线的一支.
的轨迹为双曲线的一支.
考点:1.圆与圆的位置关系;2.双曲线的定义.

练习册系列答案
相关题目
若圆C: 关于直线
关于直线 对称,则由点
对称,则由点 向圆所作的切线长的最小值是( )
向圆所作的切线长的最小值是( )
| A.2 | B. 4 | C.3 | D.6 |
点 到圆
到圆 上的点的距离的最小值是( )
上的点的距离的最小值是( )
| A.1 | B.4 | C.5 | D.6 |
已知圆 的圆心是直线
的圆心是直线 与
与 轴的交点,且圆
轴的交点,且圆 与直线
与直线 相切,则圆
相切,则圆 的方程是( )
的方程是( )
A. | B. |
C. | D. |
已知圆的半径为2,圆心在 轴的正半轴上,且与
轴的正半轴上,且与 轴相切,则圆的方程是( )
轴相切,则圆的方程是( )
A. | B. |
C.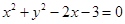 | D. |
直线 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.无法确定 |
圆C1:x2+y2+2x-3=0和圆C2:x2+y2-4y+3=0的位置关系为( )
| A.相离 | B.相交 | C.外切 | D.内含 |




 中,直线
中,直线 与圆
与圆 相交于A、B两点,则弦AB的长等于 ( )
相交于A、B两点,则弦AB的长等于 ( ) B.
B. C.
C. D.1
D.1