题目内容
圆C1:x2+y2+2x-3=0和圆C2:x2+y2-4y+3=0的位置关系为( )
| A．相离 | B．相交 | C．外切 | D．内含 |
B
解析
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
已知动圆
与圆
和圆
都外切,则动圆圆心的轨迹是（ ）
| A．圆 | B．椭圆 | C．双曲线 | D．双曲线的一支 |
若
为圆
的弦
的中点，则直线的方程是（ ）
A． | B． |
C． | D． |
若圆
上的任意一点关于直线
的对称点仍在圆上，则
最小值为（ ）
A． | B． | C． | D． |
圆x2+y2+2x=0和x2+y2﹣4y=0的公共弦的长度为（ ）
A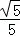． | B． | C． | D． |
已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程为( )
| A．x2+y2=2 | B．x2+y2=4 |
| C．x2+y2=2(x≠±2) | D．x2+y2=4(x≠±2) |
从原点向圆x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为( )
| A．π | B．2π | C．4π | D．6π |
点P(4,-2)与圆x2+y2=4上任一点连线的中点的轨迹方程是( )
| A．(x-2)2+(y+1)2=1 | B．(x-2)2+(y+1)2=4 |
| C．(x+4)2+(y-2)2=4 | D．(x+2)2+(y-1)2=1 |
直线l：y＝k(x－2)＋2与圆C：x2＋y2－2x－2y＝0相切，则直线l的斜率为( )．
| A．－1 | B．－2 | C．1 | D．2 |