题目内容
 (2009•南通二模)如图,在四棱椎P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,
(2009•南通二模)如图,在四棱椎P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,(1)若点E是CD上的动点,求三棱椎E-PAB体积;
(2)若E是CD的中点,F是PD上一点,PE与AF成60°角,求
| FD | PD |
分析:(1)利用转化思想把三棱椎E-PAB体积转化为三棱锥P-ABE的体积,然后直接代入体积公式求解;
(2)分别以AB、AD、AP为x、y、z轴建立坐标系,设
=m,把F点的坐标用含有m的代数式表示,利用空间向量所成的角求解运算.
(2)分别以AB、AD、AP为x、y、z轴建立坐标系,设
| FD |
| PD |
解答: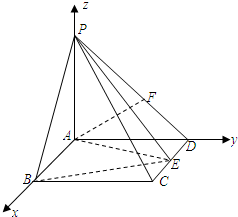 解:(1)∵PA⊥平面ABCD,△ABE是定值,
解:(1)∵PA⊥平面ABCD,△ABE是定值,
∴VE-PAB=VP-ABE=
S△ABE•PA=
×
×1×2×1=
;
(2)分别以AB、AD、AP为x、y、z轴建立坐标系(如图),
则由题知:A(0,0,0),P(0,0,1),E为CD中点,CD=2,E(1,1,0),
=(1,1,-1)
设
=m,F(0,1-m,m)(0≤m≤1),
=(0,1-m,m)
PE与AF成60°角,则|
|=
即|
|=
化简得10m2-10m+1=0,m=
±
经检验,均满足0≤m≤1,故
=
±
 解:(1)∵PA⊥平面ABCD,△ABE是定值,
解:(1)∵PA⊥平面ABCD,△ABE是定值,∴VE-PAB=VP-ABE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)分别以AB、AD、AP为x、y、z轴建立坐标系(如图),
则由题知:A(0,0,0),P(0,0,1),E为CD中点,CD=2,E(1,1,0),
| PE |
设
| FD |
| PD |
| AF |
PE与AF成60°角,则|
| ||||
|
|
| 1 |
| 2 |
即|
| 1-2m | ||||
|
| 1 |
| 2 |
化简得10m2-10m+1=0,m=
| 1 |
| 2 |
| ||
| 10 |
经检验,均满足0≤m≤1,故
| FD |
| PD |
| 1 |
| 2 |
| ||
| 10 |
点评:本题考查了直线与平面垂直的性质,考查了数学转化思想方法,训练了等积法,考查了利用空间向量求异面直线所成的角,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2009•南通二模)如图,三棱柱的侧棱长和底边长均为4,且侧棱AA1⊥面A1B1C1,正视图是边长为4的正方形,该三棱柱的左视图面积为
(2009•南通二模)如图,三棱柱的侧棱长和底边长均为4,且侧棱AA1⊥面A1B1C1,正视图是边长为4的正方形,该三棱柱的左视图面积为