题目内容
已知函数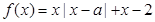 在
在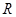 上恒为增函数,则
上恒为增函数,则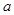 的取值范围是
的取值范围是
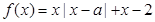 在
在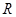 上恒为增函数,则
上恒为增函数,则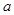 的取值范围是
的取值范围是 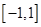
本题考查函数的单调性以及分类讨论方法。
当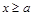 时,
时,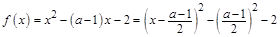 ,这是一条对称轴为直线
,这是一条对称轴为直线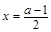 ,开口向上的抛物线,当
,开口向上的抛物线,当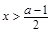 时函数递增,且
时函数递增,且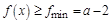 .函数
.函数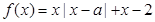 在
在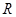 上恒为增函数,则有
上恒为增函数,则有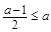 ,解得
,解得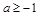 ;
;
当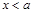 时,
时,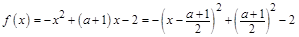 ,这是一条对称轴为直线
,这是一条对称轴为直线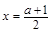 ,开口向下的抛物线,当
,开口向下的抛物线,当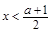 时函数递增,且
时函数递增,且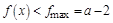 .函数
.函数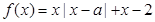 在
在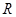 上恒为增函数,则有
上恒为增函数,则有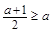 ,解得
,解得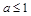 .
.
函数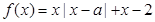 在
在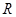 上恒为增函数,则
上恒为增函数,则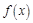 在
在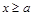 时的最小值不小于
时的最小值不小于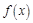 在
在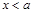 时的最大值,即
时的最大值,即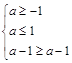 ,解得
,解得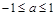 .
.
当
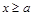 时,
时,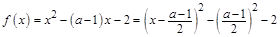 ,这是一条对称轴为直线
,这是一条对称轴为直线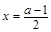 ,开口向上的抛物线,当
,开口向上的抛物线,当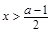 时函数递增,且
时函数递增,且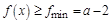 .函数
.函数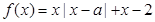 在
在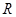 上恒为增函数,则有
上恒为增函数,则有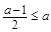 ,解得
,解得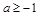 ;
;当
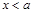 时,
时,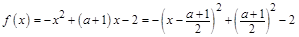 ,这是一条对称轴为直线
,这是一条对称轴为直线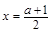 ,开口向下的抛物线,当
,开口向下的抛物线,当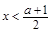 时函数递增,且
时函数递增,且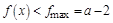 .函数
.函数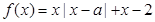 在
在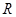 上恒为增函数,则有
上恒为增函数,则有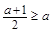 ,解得
,解得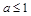 .
.函数
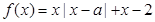 在
在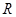 上恒为增函数,则
上恒为增函数,则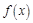 在
在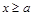 时的最小值不小于
时的最小值不小于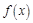 在
在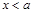 时的最大值,即
时的最大值,即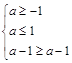 ,解得
,解得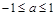 .
.
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
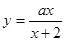 在点
在点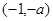 处的切线方程为
处的切线方程为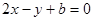 ,则
,则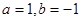
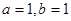
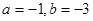
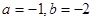
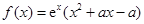 ,其中
,其中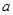 是常数.
是常数.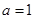 时,求
时,求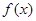 在点
在点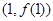 处的切线方程;
处的切线方程;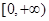 上的最小值.
上的最小值.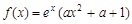
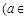 R).
R).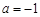 ,求曲线
,求曲线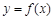 在点
在点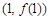 处的的切线方程;
处的的切线方程; 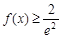 对任意
对任意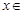
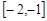 恒成立,求实数
恒成立,求实数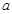 的取值范围.
的取值范围.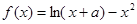 ,
,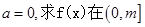
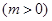 上的最大值
上的最大值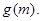
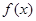 在区间[1,2]上为减函数,求a的取值范围。
在区间[1,2]上为减函数,求a的取值范围。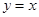 为函数
为函数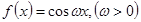 将
将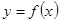 的图象向右平移
的图象向右平移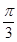 个单位长
个单位长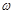 的最小值等于( )
的最小值等于( )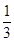
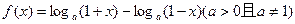
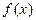 的奇偶性与单调性;
的奇偶性与单调性;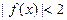 的解集为
的解集为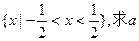 的值;
的值;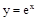 在点
在点 处的切线与坐标轴所围三角形的面积( )
处的切线与坐标轴所围三角形的面积( )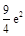
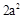
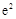
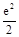
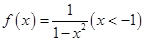 ,则
,则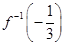 的值是( )
的值是( )