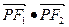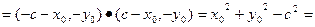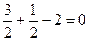题目内容
已知椭圆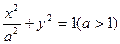 的上顶点为
的上顶点为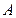 ,左右焦点分别为
,左右焦点分别为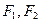 ,直线
,直线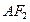 与圆
与圆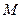 :
: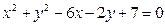 相切,若椭圆上点
相切,若椭圆上点 使得
使得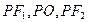 成等比数列
成等比数列
求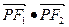
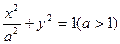 的上顶点为
的上顶点为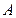 ,左右焦点分别为
,左右焦点分别为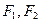 ,直线
,直线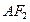 与圆
与圆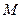 :
: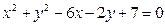 相切,若椭圆上点
相切,若椭圆上点 使得
使得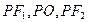 成等比数列
成等比数列求
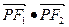
0
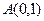 ,
,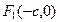 ,
,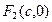 ,设直线
,设直线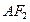 的方程为
的方程为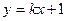 ,即
,即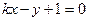
圆的方程为
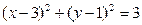 ,圆和直线相切
,圆和直线相切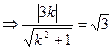
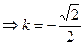
直线方程为
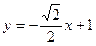 ,故
,故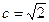 ,
,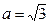 ,
,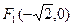 ,
,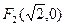
设
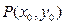 ,则
,则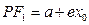 ,
,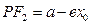 ,
,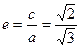 ,由已知
,由已知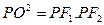
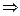
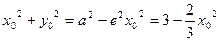 ,联立
,联立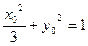
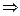
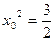 ,
,
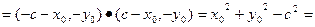
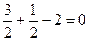

练习册系列答案
相关题目
题目内容
 的上顶点为
的上顶点为 ,左右焦点分别为
,左右焦点分别为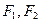 ,直线
,直线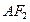 与圆
与圆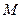 :
: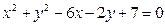 相切,若椭圆上点
相切,若椭圆上点 使得
使得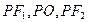 成等比数列
成等比数列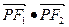
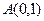 ,
,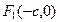 ,
,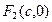 ,设直线
,设直线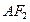 的方程为
的方程为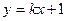 ,即
,即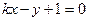
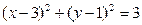 ,圆和直线相切
,圆和直线相切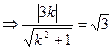
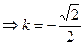
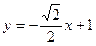 ,故
,故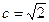 ,
,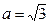 ,
,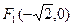 ,
,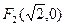
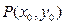 ,则
,则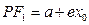 ,
,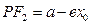 ,
,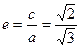 ,由已知
,由已知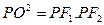
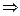
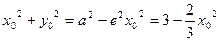 ,联立
,联立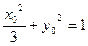
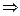
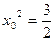 ,
,