题目内容
如图,△OBC的在个顶点坐标分别为(0,0)、(1,0)、(0,2),设P为线段BC的中点,P为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n,Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn),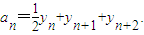
(Ⅰ)求a1,a2,a3及an;
(Ⅱ)证明
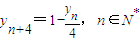 ;
;(Ⅲ)若记bn=y4n+4-y4n,n∈N*,证明{bn}是等比数列.
【答案】分析:(Ⅰ)由题意可知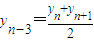 ,由此可推导出an=a1=2,n∈N*.
,由此可推导出an=a1=2,n∈N*.
(Ⅱ)将等式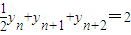 两边除以2,得
两边除以2,得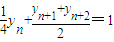 ,由此可知
,由此可知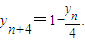
(Ⅲ)由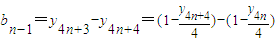 =
=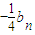 和
和 ,知{bn}是公比为
,知{bn}是公比为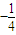 的等比数列.
的等比数列.
解答:解:(Ⅰ)因为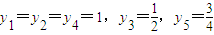 ,
,
所以a1=a2=a3=2,又由题意可知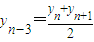
∴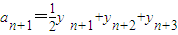
=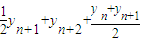
=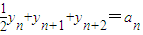 ,
,
∴{an}为常数列
∴an=a1=2,n∈N*.
(Ⅱ)将等式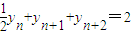 两边除以2,得
两边除以2,得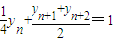 ,
,
又∵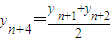
∴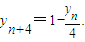
(Ⅲ)∵
=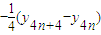
=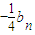 ,
,
又∵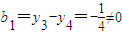 ,
,
∴{bn}是公比为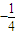 的等比数列.
的等比数列.
点评:本题考查数列的性质和综合运用,解题时要注意公式的灵活运用.
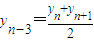 ,由此可推导出an=a1=2,n∈N*.
,由此可推导出an=a1=2,n∈N*.(Ⅱ)将等式
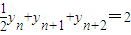 两边除以2,得
两边除以2,得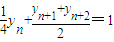 ,由此可知
,由此可知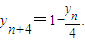
(Ⅲ)由
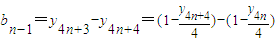 =
=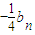 和
和 ,知{bn}是公比为
,知{bn}是公比为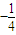 的等比数列.
的等比数列.解答:解:(Ⅰ)因为
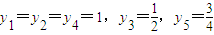 ,
,所以a1=a2=a3=2,又由题意可知
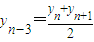
∴
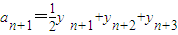
=
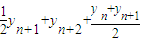
=
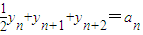 ,
,∴{an}为常数列
∴an=a1=2,n∈N*.
(Ⅱ)将等式
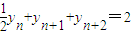 两边除以2,得
两边除以2,得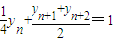 ,
,又∵
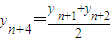
∴
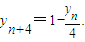
(Ⅲ)∵

=
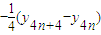
=
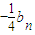 ,
,又∵
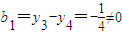 ,
,∴{bn}是公比为
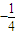 的等比数列.
的等比数列.点评:本题考查数列的性质和综合运用,解题时要注意公式的灵活运用.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目


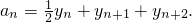
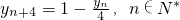 ;
;