题目内容
8.已知曲线C上的任意点M(x,y)与两个定点O(0,0),A(3,0)的距离的比为$\frac{1}{2}$(1)求曲线C的方程;
(2)已知直线x-y+2=0与曲线C交于E,F两点,求三角形EOF的面积.
分析 (1)由题意可得:$\frac{|MO|}{|MA|}=\frac{1}{2}$,可得$\frac{\sqrt{{x}^{2}+{y}^{2}}}{\sqrt{(x-3)^{2}+{y}^{2}}}=\frac{1}{2}$,化简即可得出;
(2)⊙C的方程为:(x-1)2+y2=4,可得圆心C到直线的距离d,利用|EF|=2$\sqrt{{r}^{2}-{d}^{2}}$.求出原点O到直线EF的距离h,利用S△OEF=$\frac{1}{2}|EF|•h$即可得出.
解答 解:(1)由题意可得:$\frac{|MO|}{|MA|}=\frac{1}{2}$,
∴$\frac{\sqrt{{x}^{2}+{y}^{2}}}{\sqrt{(x-3)^{2}+{y}^{2}}}=\frac{1}{2}$,化简得:x2+y2+2x-3=0;
(2)⊙C的方程为:(x-1)2+y2=4,圆心C(-1,0),半径r=2.
∴圆心C到直线的距离d=$\frac{|-1+2|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴|EF|=2$\sqrt{{r}^{2}-{d}^{2}}$=$2\sqrt{4-(\frac{\sqrt{2}}{2})^{2}}$=$\sqrt{14}$.
原点O到直线EF的距离h=$\frac{|0+2|}{\sqrt{2}}$=$\sqrt{2}$,
∴S△OEF=$\frac{1}{2}|EF|•h$=$\frac{1}{2}×\sqrt{14}×\sqrt{2}$=$\sqrt{7}$.
点评 本题考查了直线与圆相交弦长、三角形面积计算公式、点到直线的距离公式、两点之间的距离,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.已知函数f(x)=(a-1)x-ax3在[-1,1]的最小值为-1,则实数a的取值范围是( )
| A. | [-1,4] | B. | [-$\frac{1}{2}$,4] | C. | [4,+∞) | D. | [-$\frac{1}{3}$,+∞) |
3.函数f(x)=$\frac{1}{3}$x3-3x2+2015在区间[$\frac{1}{2}$,3]上的最小值为( )
| A. | 1997 | B. | 1999 | C. | 2012 | D. | 2016 |
20.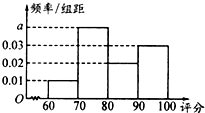 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测并评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测并评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.
(I)已知200个合格零件的评分结果的频率分布直方图如图所示.请根据此频率分布直方图,估计这200个零件评分结果的平均数和中位数;
(Ⅱ)根据已有的经验,可能被修复的零件个体被修复的概率如表:
假设每个零件被修复与否相互独立.现有5个零件的评分结果
为(单位:分):38,43,45,52,58,记这5个零件被修复的个数为随机变量X,求X的分布列和数学期望.
 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测并评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测并评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.(I)已知200个合格零件的评分结果的频率分布直方图如图所示.请根据此频率分布直方图,估计这200个零件评分结果的平均数和中位数;
(Ⅱ)根据已有的经验,可能被修复的零件个体被修复的概率如表:
| 零件评分结果所在区间 | (40,50] | (50,60] |
| 每个零件个数被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
为(单位:分):38,43,45,52,58,记这5个零件被修复的个数为随机变量X,求X的分布列和数学期望.
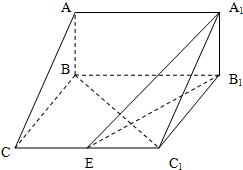 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知AA1=2,AB=$\sqrt{2}$,BC=1,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知AA1=2,AB=$\sqrt{2}$,BC=1,∠BCC1=$\frac{π}{3}$.