题目内容
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左右焦点,且椭圆
的左右焦点,且椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过
过![]() 时
时![]() 周长为8.
周长为8.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,是否存在定圆
,是否存在定圆![]() ,使得动直线
,使得动直线![]() 与之相切,若存在写出圆的方程,并求出
与之相切,若存在写出圆的方程,并求出![]() 的面积的取值范围;若不存在,请说明理由.
的面积的取值范围;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,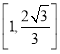 .
.
【解析】
(Ⅰ)由题意可得,![]() ,
,![]() ,从而求出答案;
,从而求出答案;
(Ⅱ)法1:设![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() ,设点
,设点![]() ,点
,点![]() ,代入椭圆方程相加得
,代入椭圆方程相加得![]() ,从而可求出
,从而可求出![]() ,可得
,可得![]() ,由此可求出答案;
,由此可求出答案;
法2:联立直线与椭圆方程得韦达定理的结论,代入到![]() 可得
可得![]() ,从而
,从而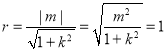 ,根据弦长公式,求出面积的范围.
,根据弦长公式,求出面积的范围.
解:(Ⅰ)由题意可得,![]() ,
,
故![]() ,又有
,又有![]() ,∴
,∴![]() ,
,
椭圆的标准方程为![]() ;
;
(Ⅱ)法1:设![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
设点![]() ,点
,点![]() ,
,
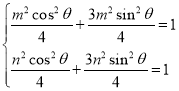 ,两式相加得
,两式相加得![]() ,
,
![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,
,![]() ,
,
∴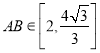 ,
, .
.
法2: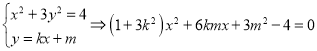 ,
,
![]() ,
,
![]()
![]()
![]() ,
,
∴![]() ,
,
∴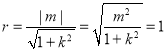 ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,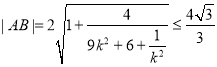 ,当且仅当
,当且仅当![]() 时取到等号,此时
时取到等号,此时![]() 符合
符合![]()
∴ .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】1772年德国的天文学家波得发现了求太阳的行星距离的法则,记地球距离太阳的平均距离为10,可以算得当时已知的六大行星距离太阳的平均距离如下表:
星名 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
与太阳的距离 | 4 | 7 | 10 | 16 | 52 | 100 |
除水星外,其余各星与太阳的距离都满足波得定则(某一数列规律),当时德国数学家高斯根据此定则推算,火星和木星之间距离太阳28还有一颗大行星,1801年,意大利天文学家皮亚齐经过观测,果然找到了火星和木星之间距离太阳28的谷神星以及它所在的小行星带,请你根据这个定则,估算从水星开始由近到远算,第10个行星与太阳的平均距离大约是( )
A.388B.772C.1540D.3076
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.