题目内容
某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗A原料l千克、B原料2千克;生产乙产品l桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是
(A)2200元 (B)2400元
(C)2600元 (D)2800元
D
解析试题分析:设生产甲产品x桶,乙产品y桶,利润为z,则有 ,
,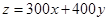
做出可行域观察可知当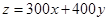 过直线
过直线 的交点
的交点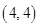 时取得最大值2800
时取得最大值2800
考点:线性规划
点评:线性规划问题取得最值的位置一般在可行域的端点处或边界处

练习册系列答案
相关题目
已知函数 若
若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设奇函数 的定义域为R,最小正周期
的定义域为R,最小正周期 ,若
,若 ,则
,则 的取值范围是
的取值范围是
A. | B. |
C. | D. |
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).求f(x)的最大值( ).
A. | B.2 |
| C.3 | D. |
点A(a+b,ab)在第一象限内,则直线bx+ay-ab=0不经过的象限是( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若 ,则有( )
,则有( )
A. | B. | C.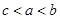 | D. |
设a>1,则log0.2a , 0.2a, a0.2的大小关系是( )
| A.0.2a<log0.2a<a0.2 | B.log0.2a<0.2a<a0.2 |
| C.log0.2a<a0.2<0.2a | D.0.2a<a0.2<log0.2a |
设函数 的定义域为
的定义域为
 ,值域为
,值域为 ,若
,若 的最小值为
的最小值为 ,则实数a的值为( )
,则实数a的值为( )
A. | B. 或 或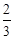 | C.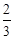 | D.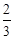 或 或 |
二次函数f(x)的二次项系数为正数,且对任意xÎR都有f(x)=f(4-x)成立,
若f(2-a2)<f(1+a-a2),那么a的取值范围是 ( )
| A.1<a<2 | B.a>1 | C.a>2 | D.a<1 |