题目内容
点A(a+b,ab)在第一象限内,则直线bx+ay-ab=0不经过的象限是( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
C
解析试题分析:根据第一象限点的横坐标大于0,纵坐标小于0,得到ab大于0且a+b大于0,即a与b都大于0,然后把直线的方程化为点斜式方程y=kx+b,判断k和b的正负即可得到直线不经过的象限解:由点A(a+b,ab)在第一象限内,得到ab>0且a+b>0,即a>0且b>0,而直线bx+ay-ab=0可化为:y=-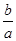 x+b,由-
x+b,由-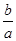 <0,b>0,得到直线不经过第三象限.故选C.
<0,b>0,得到直线不经过第三象限.故选C.
考点:一次函数的图象
点评:此题考查学生掌握一次函数的图象与性质,掌握象限角的特点,是一道基础题.

练习册系列答案
相关题目
若函数 是定义在
是定义在 上的偶函数,在
上的偶函数,在 上是减函数,且
上是减函数,且 ,则使得
,则使得 的
的 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
已知函数 则
则 的值为
的值为
| A.-1 | B.-2 | C.1 | D.2 |
若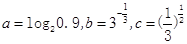 ,
,
A. | B. |
C. | D. |
若 ,则P,Q的大小关系为
,则P,Q的大小关系为
A. | B. | C. | D. |
函数 的定义域是 ( )
的定义域是 ( )
| A.[-1,1] | B.(-1,1) |
| C.(1 ,+∞) | D.(-∞,2)∪(2,+∞) |
已知 ,
, =( )
=( )
A. | B.0 | C.1 | D.2 |
已知 ,则f(3)为 ( )
,则f(3)为 ( )
| A.2 | B. 3 | C. 4 | D.5 |