题目内容
设奇函数 的定义域为R,最小正周期
的定义域为R,最小正周期 ,若
,若 ,则
,则 的取值范围是
的取值范围是
A. | B. |
C. | D. |
C
解析试题分析:根据函数的周期为3且为奇函数,得f(2)=f(-1)=-f(1)≤-1,解之即得实数a的取值范围.解:∵f(x)的最小正周期T=3,∴f(2)=f(2-3)=f(-1),∵奇函数f(x)满足f(-x)=-f(x),∴f(-1)=-f(1)≤-1,即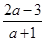 ≤-1,解之得:-1<a≤
≤-1,解之得:-1<a≤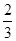 故答案为:-1<a≤
故答案为:-1<a≤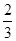 ,故选C.
,故选C.
考点:
点评:本题给出周期为3的奇函数,求解关于x的不等式,着重考查了函数的周期性、奇偶性和分式不等式的解法等知识,属于基础题.

练习册系列答案
相关题目
如果函数 的定义域为
的定义域为 ,则实数
,则实数 的值为( )
的值为( )
A.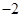 | B. | C. | D. |
已知函数 若有
若有 则
则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
已知函数 则
则 的值为
的值为
| A.-1 | B.-2 | C.1 | D.2 |
设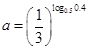 ,
, ,
, ,则
,则 的大小关系是
的大小关系是
A. | B. | C.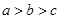 | D. |
若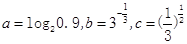 ,
,
A. | B. |
C. | D. |
设 ,且
,且 ,则
,则
A. | B.10 | C.20 | D.100 |



