Question

15．求函数f（x）=|x²-2ax|+2x的最小值．

Answer 1

分析 先将函数的解析式化为分段函数的形式，再结合二次函数的图象和性质，分别讨论不同情况下，函数的最小值，最后综合讨论结果，可得答案．

解答 解：当a＜0时，函数f（x）=|x²-2ax|+2x=$\left\{\begin{array}{l}{x}^{2}+（2-2a）x，x＜2a，或x＞0\\-{x}^{2}+（2+2a）x，2a≤x≤0\end{array}\right.$，
当-1＜a＜0时，函数草图如下所示：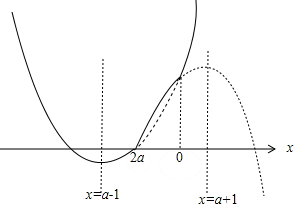

此时当x=a-1时，函数取最小值-（a-1）²；
当a≤-1时，函数草图如下所示：

此时当x=0时，函数取最小值0；
当a=0时，函数f（x）=|x²-2ax|+2x=x²+2x，当x=-1时，函数取最小值-1；
当a＞0时，函数f（x）=|x²-2ax|+2x=$\left\{\begin{array}{l}{x}^{2}+（2-2a）x，x＜0，或x＞2a\\-{x}^{2}+（2+2a）x，0≤x≤2a\end{array}\right.$，
当0＜a＜1时，函数草图如下所示：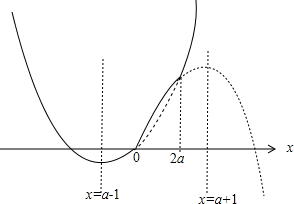

此时当x=a-1时，函数取最小值-（a-1）²；
当a≥1时，函数草图如下所示：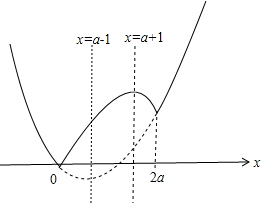

此时当x=0时，函数取最小值0；
综上所述，函数f（x）=|x²-2ax|+2x的最小值为$\left\{\begin{array}{l}-（a-1）^{2}，-1＜a＜1\\ 0，a≤-1，或a≥1\end{array}\right.$

点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．