题目内容

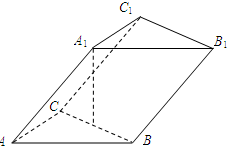如图：已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等，过顶点A1作底面ABC的垂线，若垂足为BC的中点，则异面直线AB与CC1成的角的余弦值为
3
4
3
4
．
分析：确定∠A1AB即为异面直线AB与CC1所成的角，再在△∠A1AB中，利用余弦定理即可求解．
解答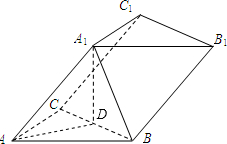：解：设BC的中点为D，连接A1D、AD、A1B，则
∵AA1∥CC1，∴∠A1AB即为异面直线AB与CC1所成的角．
设三棱柱ABC-A1B1C1的侧棱与底面边长为1，则|AD|=
3
2
，|A1D|=
1
2
，|A1B|=
2
2

由余弦定理，得cos∠A1AB=
1+1-
1
2
2
=
3
4

故答案为：
3
4
点评：本题考查线线角，考查余弦定理的运用，解题的关键是确定线线角．
练习册系列答案
相关题目
精英家教网如图，已知三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AC=BC=2，AA1=4，AB=2
2
，M，N分别是棱CC1，AB中点．
（Ⅰ）求证：CN⊥平面ABB1A1；
（Ⅱ）求证：CN∥平面AMB1；
（Ⅲ）求三棱锥B1-AMN的体积．
精英家教网如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，且AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足
A1P
=λ
A1B1
．
（1）证明：PN⊥AM；
（2）当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该角最大值的正切值．
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，M，N分别是CC1，BC的中点，点P在直线A1B1上，且
A1P
=λ
A1B1
；
（Ⅰ）证明：无论λ取何值，总有AM⊥PN；
（Ⅱ）当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该角取最大值时的正切值；
（Ⅲ）是否存在点P，使得平面PMN与平面ABC所成的二面角为30°，若存在，试确定点P的位置，若不存在，请说明理由．
如图，已知三棱柱ABC-A1B1C1的所有棱长均为2，且A1A⊥底面ABC，D为AB的中点，G为△ABC1的重心，则|
CG
|的值为（　　）
精英家教网如图，已知三棱柱ABC-A1B1C1中，AA1⊥平面ABC，AB=BC，∠ABC=90°，D为AC中点．
（1）求证：BD⊥AC1；
（2）若AB=
2
，AA1=2
3
，求AC1与平面ABC所成的角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网