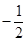题目内容
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为(
,-
),∠AOC=α.
(Ⅰ)求圆O的半径及C点的坐标;
(Ⅱ)若|BC|=1,求
cos2
-sin
cos
-
的值.

| 4 |
| 5 |
| 3 |
| 5 |
(Ⅰ)求圆O的半径及C点的坐标;
(Ⅱ)若|BC|=1,求
| 3 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| ||
| 2 |

(Ⅰ)半径r=|OB|=
=1,(2分)
点C的坐标为(cosα,sinα);(5分)
(Ⅱ)由(1)可知|OB|=|OC|=|BC|=1,∴∠BOC=
(6分)
cos2
-sin
cos
-
=
(
)-
sinα-
=
cosα-
sinα=sin(
-α)=sin∠BOA=
(13分)
(
|
点C的坐标为(cosα,sinα);(5分)
(Ⅱ)由(1)可知|OB|=|OC|=|BC|=1,∴∠BOC=
| π |
| 3 |
| 3 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| ||
| 2 |
=
| 3 |
| cosα+1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3 |
| 5 |

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 ,
, ,且
,且
 的取值范围;
的取值范围; ,试求
,试求 的取小值,并求此时
的取小值,并求此时 的值。
的值。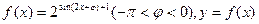 的图象的一条对称轴是直线
的图象的一条对称轴是直线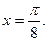
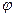 ;
;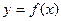 的递减区间;
的递减区间;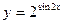 的图象作怎样变换得到.
的图象作怎样变换得到.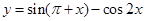 ,则
,则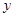 的最小值和最大值分别为( )
的最小值和最大值分别为( )





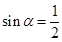 ,则
,则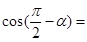 ( )
( )