题目内容
 (2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1.
(2007•河东区一模)已知:正方体ABCD-A1B1C1D1的棱长为1.(Ⅰ)求棱AA1与平面A1BD所成的角;
(Ⅱ)求二面角B-A1D-B1的大小;
(Ⅲ)求四面体A1-BB1D的体积.
分析:(Ⅰ)取BD的中点O,连结OA,OA1.证出∠AA1O为AA1与平面A1BD所成的角.并求解.
(Ⅱ)取B1C的中点E,A1D的中点F,连结BE、EF、FB.证出∠BFE为二面角B-A1D-B1的平面角.
在Rt△BEF中求解.
(Ⅲ)利用体积转化法求四面体A1-BB1D的体积.V=V B--A1B1D=V B-B1DC=V D-BCB1
(Ⅱ)取B1C的中点E,A1D的中点F,连结BE、EF、FB.证出∠BFE为二面角B-A1D-B1的平面角.
在Rt△BEF中求解.
(Ⅲ)利用体积转化法求四面体A1-BB1D的体积.V=V B--A1B1D=V B-B1DC=V D-BCB1
解答: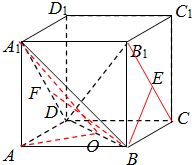 解:(Ⅰ)取BD的中点O,连结OA,OA1.
解:(Ⅰ)取BD的中点O,连结OA,OA1.
∵四边形ABCD为正方形,∴AO⊥BD,
又AA1⊥BD,∴BD⊥平面AA1O,
∴AA1在平面A1BD上的射影落在OA1上,
∴∠AA1O为AA1与平面A1BD所成的角.
∵AA1=1,AO=
,∴tan∠AA1O=
,∴∠AA1O=arctan
.----4分
(Ⅱ)取B1C的中点E,A1D的中点F,连结BE、EF、FB.
∵△A1BD为正三角形,∴BF⊥A1O,
又四边形A1B1CD是矩形,∴EF⊥A1D,
∴∠BFE为二面角B-A1D-B1的平面角.
∵EF∥A1B1,A1B1⊥平面BC1,∴EF⊥BF.
在Rt△BEF中,BE=
,EF=1,∴tan∠BFE=
,
∴∠BFE=arctan
.-----------------------------------------------------------------8分
(Ⅲ)(Ⅲ)四面体A1-BB1D的体积V=V B--A1B1D=V B-B1DC=V D-BCB1=
×
×1×1×1=
.--12分.
 解:(Ⅰ)取BD的中点O,连结OA,OA1.
解:(Ⅰ)取BD的中点O,连结OA,OA1.∵四边形ABCD为正方形,∴AO⊥BD,
又AA1⊥BD,∴BD⊥平面AA1O,
∴AA1在平面A1BD上的射影落在OA1上,
∴∠AA1O为AA1与平面A1BD所成的角.
∵AA1=1,AO=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(Ⅱ)取B1C的中点E,A1D的中点F,连结BE、EF、FB.
∵△A1BD为正三角形,∴BF⊥A1O,
又四边形A1B1CD是矩形,∴EF⊥A1D,
∴∠BFE为二面角B-A1D-B1的平面角.
∵EF∥A1B1,A1B1⊥平面BC1,∴EF⊥BF.
在Rt△BEF中,BE=
| ||
| 2 |
| ||
| 2 |
∴∠BFE=arctan
| ||
| 2 |
(Ⅲ)(Ⅲ)四面体A1-BB1D的体积V=V B--A1B1D=V B-B1DC=V D-BCB1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查空间角大小体积的求解,考查空间想象能力、推理论证、计算、转化能力.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目