题目内容
已知平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AA1=AB=AD=1,E为A1D1的中点。

给出下列四个命题:①∠BCC1为异面直线 与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④ ;⑤|
;⑤| |=
|= .其中正确的命题有_____________.(写出所有正确命题的序号)
.其中正确的命题有_____________.(写出所有正确命题的序号)
【答案】
②④⑤
【解析】
试题分析::①∵∠BCC1为120°,而异面直线AD与CC1所成的角为60°,故①错误;
②三棱锥A1-ABD的每个面都为正三角形,故为正四面体,故②正确;
④根据向量加法的三角形法则,
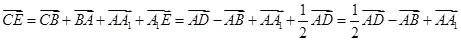 ,故④正确;
,故④正确;
③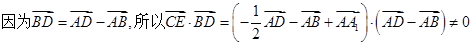 ,所以CE与BD不垂直,故③错误;
,所以CE与BD不垂直,故③错误;
⑤在三角形ACC1中,
 ,所以|
,所以|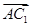 |=
|=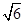 。
。
考点:空间向量基本定理及意义;异面直线所成的角;直线与平面垂直的判断;棱柱的结构特征。
点评:本题考查了异面直线所成的角的定义,直线与平面垂直的定义,正三棱锥的定义,向量加法的三角形法则和数量积运算性质,知识点较为综合,我们应熟练掌握每一个知识点。

练习册系列答案
相关题目
 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.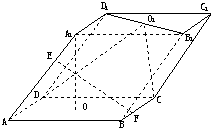 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.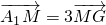 ,设
,设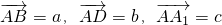 ,用向量a、b、c表示向量
,用向量a、b、c表示向量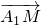 ;
;