题目内容
 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.
(I)若G为△ABC的重心,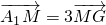 ,设
,设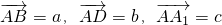 ,用向量a、b、c表示向量
,用向量a、b、c表示向量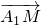 ;
;
(II)若平行六面体ABCD-A1B1C1D1各棱长相等且AB⊥平面BCC1B1,E为CD中点,AC1∩BD1=O,求证;OE⊥平面ABC1D1.
解:(I)依题意,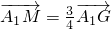 =
=
∵G为△ABC的重心,
∴ =
= ×
×
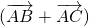 =
=
又∵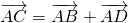
∴ [
[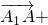
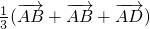 ]
]
=
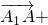
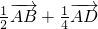
=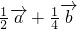 -
-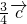
(II)证明:连接C1E,AE,
∵平行六面体ABCD-A1B1C1D1各棱长相等且AB⊥平面BCC1B1
∴C1E=AE,
∴△C1EA为等腰三角形
∵O为AC1的中点,
∴OE⊥AC1
同理可证 OE⊥BD1
∵AC1∩BD1=O,
∴OE⊥平面ABC1D1.
分析:(I)利用向量加法的三角形法则及重心的性质,将 用基底表示,再在三角形A1AG中,将
用基底表示,再在三角形A1AG中,将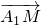 用基底表示;
用基底表示;
(II)连接C1E,AE,由已知证明△C1EA为等腰三角形,从而OE⊥AC1,同理可证明OE⊥BD1,最后由线面垂直的判定定理证明结论
点评:本题考查了空间向量的基本定理及其应用,向量加法的三角形法则,重心的性质及线面垂直的判定定理
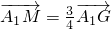 =
=
∵G为△ABC的重心,
∴
 =
= ×
×
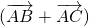 =
=
又∵
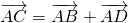
∴
 [
[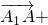
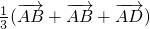 ]
]=

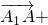
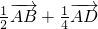
=
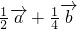 -
-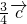
(II)证明:连接C1E,AE,
∵平行六面体ABCD-A1B1C1D1各棱长相等且AB⊥平面BCC1B1
∴C1E=AE,
∴△C1EA为等腰三角形
∵O为AC1的中点,
∴OE⊥AC1
同理可证 OE⊥BD1
∵AC1∩BD1=O,
∴OE⊥平面ABC1D1.
分析:(I)利用向量加法的三角形法则及重心的性质,将
 用基底表示,再在三角形A1AG中,将
用基底表示,再在三角形A1AG中,将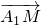 用基底表示;
用基底表示;(II)连接C1E,AE,由已知证明△C1EA为等腰三角形,从而OE⊥AC1,同理可证明OE⊥BD1,最后由线面垂直的判定定理证明结论
点评:本题考查了空间向量的基本定理及其应用,向量加法的三角形法则,重心的性质及线面垂直的判定定理

练习册系列答案
相关题目
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱) 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.