Question

已知a∈R，函数f（x）=x|x-a|，
（Ⅰ）当a=2时，写出函数y=f（x）的单调递增区间；
（Ⅱ）当a＞2时，求函数y=f（x）在区间[1，2]上的最小值；
（Ⅲ）设a≠0，函数f（x）在（m，n）上既有最大值又有最小值，请分别求出m、n的取值范围（用a表示）．

Answer 1

分析：（I）将a=2代入函数的解析得出f（x）=x|x-2|，将其变为分段函数，利用二次函数的图象与性质研究其单调性即可
（Ⅱ）当a＞2时，函数y=f（x）在区间[1，2]上解析式是确定的，去掉绝对号后根据二次函数的性质确定其单调性，再求最值．
（Ⅲ）a≠0，函数f（x）在（m，n）上既有最大值又有最小值说明在函数最值不在区间端点处取得，在这个区间内必有两个极值，由函数的性质确定出极值，由于极值即为最值，故可借助函数的图象得m、n的取值范围．

解答：解：（Ⅰ）当a=2时，f（x）=x|x-2|=

x(x-2)，x≥2 x(2-x)，x＜2

由二次函数的性质知，单调递增区间为（-∞，1]，[2，+∞）（开区间不扣分）
（Ⅱ）因为a＞2，x∈[1，2]时，所以f（x）=x（a-x）=-x²+ax=-(x-

a

2

)2+

a2

4

当1＜

a

2

≤

3

2

，即2＜a≤3时，f（x）_min=f（2）=2a-4
当

a

2

＞

3

2

，即a＞3时，f（x）_min=f（1）=a-1
∴f(x)min=

2a-4，2＜a≤3 a-1，a＞3

（Ⅲ）f(x)=

x(x-a)，x≥a x(a-x)，x＜a

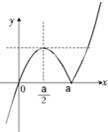
①当a＞0时，图象如上图左所示
由

y= a2 4 y=x(x-a)

得x=

( 2 +1)a

2

∴0≤m＜

a

2

，a＜n≤

2 +1

2

a
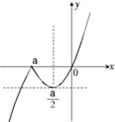
②当a＜0时，图象如上图右所示
由

y=- a2 4 y=x(a-x)

得x=

(1+ 2)

2

a
∴

1+ 2

2

a≤m＜a，

a

2

＜n≤0

点评：本题考点是函数的最值及其几何意义，综合考查了二次函数的图象，最值等知识以及配方法求最值的技巧．解题时数形结合，转化灵活，综合性很强．