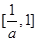题目内容
已知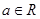 ,函数
,函数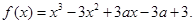
(1)求曲线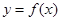 在点
在点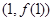 处的切线方程; (2)当
处的切线方程; (2)当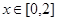 时,求
时,求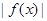 的最大值.
的最大值.
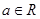 ,函数
,函数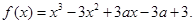
(1)求曲线
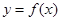 在点
在点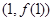 处的切线方程; (2)当
处的切线方程; (2)当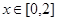 时,求
时,求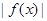 的最大值.
的最大值.(1)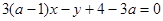 ,(2)
,(2)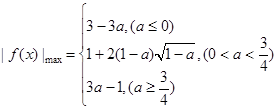
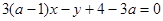 ,(2)
,(2)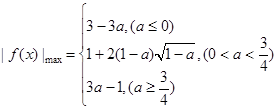
试题分析:(1)导数几何意义即切线的斜率;(2)求导数,列表判断单调性,分情况讨论.
试题解析:(Ⅰ)由已知得:
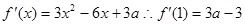 ,且
,且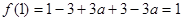 ,所以所求切线方程为:
,所以所求切线方程为: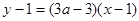 ,
,即为:
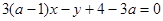 ;
; (Ⅱ)由已知得到:
 ,其中
,其中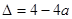 ,当
,当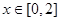 时,
时,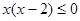 ,
, (1)当
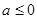 时,
时,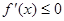 ,所以
,所以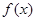 在
在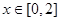 上递减,所以
上递减,所以 ,因为
,因为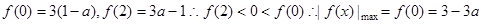 ;
; (2)当
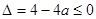 ,即
,即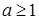 时,
时,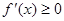 恒成立,所以
恒成立,所以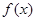 在
在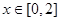 上递增,所以
上递增,所以 ,因为
,因为  ;
; (3)当
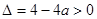 ,即
,即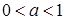 时,
时, 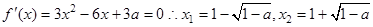 ,且
,且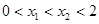 ,即
,即 |  | 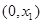 | 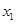 | 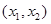 | 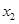 | 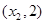 | 2 |
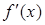 | | + | 0 | - | 0 | + | |
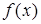 | 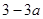 | 递增 | 极大值 | 递减 | 极小值 | 递增 | 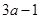 |
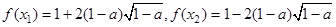 ,且
,且  所以
所以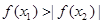 ,
, 所以
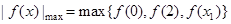 ;
; 由
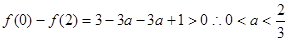 ,所以
,所以 (ⅰ)当
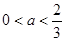 时,
时,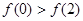 ,所以
,所以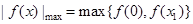 ,因为
,因为 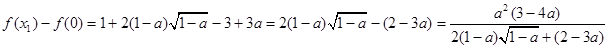 ,又因为
,又因为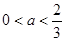 ,所以
,所以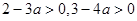 ,所以
,所以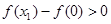 ,所以
,所以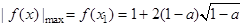
(ⅱ)当
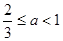 时,
时,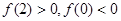 ,所以
,所以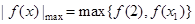 ,因为
,因为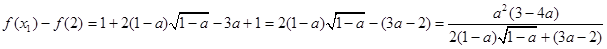 ,此时
,此时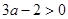 ,当
,当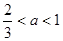 时,
时,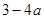 是大于零还是小于零不确定,所以
是大于零还是小于零不确定,所以 ① 当
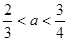 时,
时,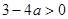 ,所以
,所以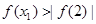 ,所以此时
,所以此时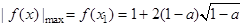 ;
; ② 当
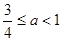 时,
时,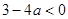 ,所以
,所以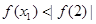 ,所以此时
,所以此时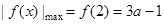
综上所述:
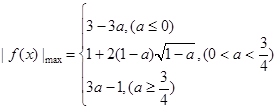

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 .
.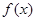 在
在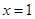 处取得极值,且函数
处取得极值,且函数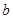 的取值范围.
的取值范围.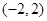 上不是单调函数,求
上不是单调函数,求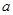 的取值范围.
的取值范围. .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;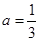 时,求函数
时,求函数 ,若对于
,若对于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求实数
成立,求实数 的取值范围.
的取值范围. 在
在 处的切线平行于直线
处的切线平行于直线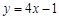 ,则
,则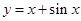 在点
在点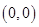 处的切线方程是 .
处的切线方程是 .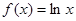 ,且
,且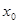 ,
,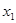 ,
,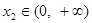 ,下列命题:
,下列命题: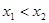 ,则
,则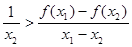
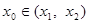 ,
,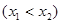 ,使得
,使得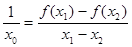
 ,
,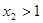 ,则
,则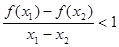
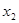 ,都有
,都有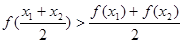
 的图像在点
的图像在点 处的切线斜率为
处的切线斜率为 ,则
,则 的值是 .
的值是 .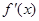 是函数f(x)的导函数,如果
是函数f(x)的导函数,如果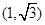
 ,那么曲线f(x)上任一点处的切线的倾斜角
,那么曲线f(x)上任一点处的切线的倾斜角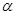 的取值范围是
的取值范围是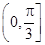
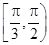
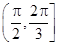
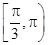
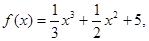 则函数
则函数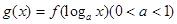 的单调递增区间是( )
的单调递增区间是( )