题目内容
【题目】设抛物线
的焦点为
，
的准线与
轴的交点为
，点
是上的动点．当
是等腰直角三角形时，其面积为2．
（1）求的方程；
（2）延长AF交C于点B，点M是C的准线上的一点，设直线
，
，
的斜率分别是
，证明：
．
【答案】（1）
（2）证明见解析
【解析】
（1）根据抛物线的准线方程和焦点坐标，结合勾股定义以及三角形面积，即可求得
，则抛物线方程可求；
（2）设出直线方程，联立抛物线方程，得到关于
的一元二次方程，将斜率之和
表示出来，结合韦达定理，即可证明.
（1）依题意可知，当
是等腰直角三角形时：
若
时，根据抛物线定义，显然不成立；
若
时，显然也不成立.
故
.
∵抛物线
方程为
，
∴焦点
，
，
∴的面积
，解得
，
∴抛物线的方程为
（2）证明：由（1）知
，
设直线
的方程：
代入得:
，
设
，所以
设
，则：
，
，
∵
，∴
∴
∴
.
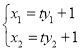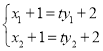
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
【题目】某险种的基本保费为
（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下：
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
（1）求一续保人本年度的保费高于基本保费的概率；
（2）已知一续保人本年度的保费高于基本保费，求其保费比基本保费高出
的概率.
