题目内容
2. 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1,
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1,∠BAC=∠BAP=120°.
(1)求证:AB⊥PC;
(2)若E为BC的中点,求直线PE与平面PAB所成角的正弦值.
分析 (1)过P作PD⊥AB,交BA的延长线于D,连接CD,利用面面垂直,线面垂直,进一步得到线线垂直;
(2)由(1)得CD⊥平面PAB,以D为原点,DB,DC,DP分别为x,y,z轴建立坐标系,利用向量$\overrightarrow{PE}$与平面PAB的法向量的夹角求值.
解答 (1)证明:过P作PD⊥AB,交BA的延长线于D,连接CD,如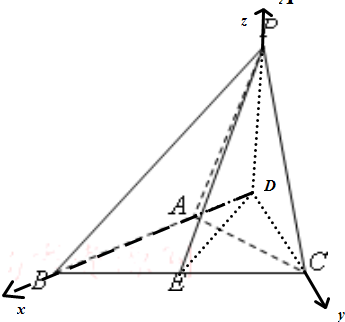 图,
图,
∵平面PAB⊥平面ABC,
∴PD⊥平面ABC,
∵PA=AB=AC=1,∠BAC=∠BAP=120°.
∴PD=PAsin60°=$\frac{\sqrt{3}}{2}$,AD=$\frac{1}{2}$,
在△ACD中,AC=1,AD=$\frac{1}{2}$,∠DAC=60°,∴∠ADC=90°,故AD⊥CD,
∴BA⊥平面PCD,
∴BA⊥PC;
(2)由(1)得CD⊥平面PAB,以D为原点,DB,DC,DP分别为x,y,z轴建立坐标系,
则D(0,0,0,),P(0,0,$\frac{\sqrt{3}}{2}$),C(0,$\frac{\sqrt{3}}{2}$,0),E($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$,0)
所以$\overrightarrow{PE}=(\frac{3}{4},\frac{\sqrt{3}}{4},-\frac{\sqrt{3}}{2})$,$\overrightarrow{DC}=(0,\frac{\sqrt{3}}{2},0)$,
cos<$\overrightarrow{PE},\overrightarrow{DC}$>=$\frac{\overrightarrow{PE}•\overrightarrow{DC}}{|\overrightarrow{PE}||\overrightarrow{DC}|}$=$\frac{\frac{3}{8}}{\frac{\sqrt{3}}{2}\sqrt{\frac{3}{2}}}=\frac{\sqrt{2}}{4}$,
所以直线PE与平面PAB所成角的正弦值为$\frac{\sqrt{2}}{4}$.
点评 本题考查了线面垂直的性质定理的运用以及利用空间向量求线面角,属于中档题.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| ξ | 1 | 3 | 5 |
| p | 0.4 | 0.1 | x |
 如图,在三棱锥S-ABC中,底面ABC是正三角形,AB=4,SA=SC=2$\sqrt{3}$,侧面SAC⊥底面ABC,D,E分别为AB,SB的中点.
如图,在三棱锥S-ABC中,底面ABC是正三角形,AB=4,SA=SC=2$\sqrt{3}$,侧面SAC⊥底面ABC,D,E分别为AB,SB的中点. 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论