题目内容
已知抛物线C的顶点在原点，焦点为（0，1）．
（Ⅰ）求抛物线C的方程；
（Ⅱ）已知直线l1：y=kx+b（b＞0）交抛物线C于A，B两点，M是线段AB的中点，过M作x轴的垂线交抛物线于点N．是否存在实数k，使点N在以AB为直径的圆上？若存在，求出k的所有的值；若不存在，说明理由．
（Ⅰ）求抛物线C的方程；
（Ⅱ）已知直线l1：y=kx+b（b＞0）交抛物线C于A，B两点，M是线段AB的中点，过M作x轴的垂线交抛物线于点N．是否存在实数k，使点N在以AB为直径的圆上？若存在，求出k的所有的值；若不存在，说明理由．
分析：（Ⅰ）设抛物线C的方程是x2=ay，根据焦点为F的坐标求得a，进而可得抛物线的方程；
（Ⅱ）将y=kx+b与x2=4y联立，设A（xA，yA），B（xB，yB），利用韦达定理得到xA+xB=4k，xAxB=-4b，结合题意可求
N（2k，k2），N在以AB为直径的圆上?
•
=0，最后可得到3k2+（4-b）=0，对b讨论即可．
（Ⅱ）将y=kx+b与x2=4y联立，设A（xA，yA），B（xB，yB），利用韦达定理得到xA+xB=4k，xAxB=-4b，结合题意可求
N（2k，k2），N在以AB为直径的圆上?
| NA |
| NB |
解答：解：（Ⅰ）设抛物线C的方程是x2=ay，
则
=1，即a=4．
故所求抛物线C的方程为x2=4y． （5分）
（Ⅱ）将y=kx+b代入x2=4y得 x2-4kx-4b=0，
设A（xA，yA），B（xB，yB），则xA+xB=4k，xAxB=-4b，（7分）
xN=xM=
=2k，代入x2=4y得yN=k2，所以N（2k，k2），
∵N在以AB为直径的圆上，
=（xA-2k，yA-k2），
=（xB-2k，yB-k2），
∴
•
=0；
∴（xA-2k）（xB-2k）+（yA-k2）（yB-k2）=0，（10分）
即（xA-2k）（xB-2k）+（
-k2）（
-k2）=0，
即（xA-2k）（xB-2k）[1+
（xA+2k）（xB+2k）]=0，
∵（xA-2k）（xB-2k）=xAxB-2k（xA+xB）+4k2=-4b-4k2=-4（b+k2），
由于b＞0，
∴（xA-2k）（xB-2k）=-4（b+k2）＜0，
∴1+
（xA+2k）（xB+2k）=
+
+
+1=0，
即：3k2+（4-b）=0…（13分）
所以，当b≥4时，存在实数k=±
；当b＜4时，不存在实数k． （15分）
则
| a |
| 4 |
故所求抛物线C的方程为x2=4y． （5分）
（Ⅱ）将y=kx+b代入x2=4y得 x2-4kx-4b=0，
设A（xA，yA），B（xB，yB），则xA+xB=4k，xAxB=-4b，（7分）
xN=xM=
| xA+xB |
| 2 |
∵N在以AB为直径的圆上，
| NA |
| NB |
∴
| NA |
| NB |
∴（xA-2k）（xB-2k）+（yA-k2）（yB-k2）=0，（10分）
即（xA-2k）（xB-2k）+（
| xA2 |
| 4 |
| xB2 |
| 4 |
即（xA-2k）（xB-2k）[1+
| 1 |
| 16 |
∵（xA-2k）（xB-2k）=xAxB-2k（xA+xB）+4k2=-4b-4k2=-4（b+k2），
由于b＞0，
∴（xA-2k）（xB-2k）=-4（b+k2）＜0，
∴1+
| 1 |
| 16 |
| xAxB |
| 16 |
| (xA+xB)k |
| 8 |
| k2 |
| 4 |
即：3k2+（4-b）=0…（13分）
所以，当b≥4时，存在实数k=±
|
点评：本题主要考查抛物线的标准方程以及抛物线与直线的关系，着重考查抛物线与直线方程的联立，韦达定理的使用，难点在于梳理点A、B、M、N坐标间的关系并合理应用，突出化归思想、方程思想、分类讨论思想的运用，是难题．
练习册系列答案
相关题目
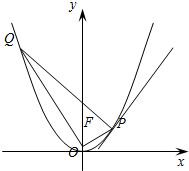已知抛物线C的顶点在原点，焦点为F（0，1）．