题目内容
已知抛物线C的顶点在原点,焦点为F(
,0).(1)求抛物线C的方程; (2)已知直线y=k(x+
) 与抛物线C交于A、B 两点,且|FA|=2|FB|,求k 的值; (3)设点P 是抛物线C上的动点,点R、N 在y 轴上,圆(x-1)2+y2=1 内切于△PRN,求△PRN 的面积最小值.
| 1 |
| 2 |
| 1 |
| 2 |
分析:(1)设抛物线C的方程为y2=2px(p>0),焦点为 F(
,0).
=
,p=1,从而可求抛物线C的方程.
(2)设A(x1,y1),B(x2,y2),由|FA|=2|FB|,得 x1-2x2=
,将直线与抛物线方程联立可得 x1+x2=
-1,x1x2=
,从而问题得解.
(3)设P(x0,y0),R(0,b),N(0,c),且b>c,则直线PR的方程可得,由题设知,圆心(1,0)到直线PR的距离为1,把x0,y0代入化简整理可得(x0-2)b2+2y0b-x0=0,同理可得(x0-2)c2+2y0c-x0=0,进而可知b,c为方程(x0-2)x2+2y0x-x0=0的两根,根据求根公式,可求得b-c,进而可得△PRN的面积的表达式,根据均值不等式可知当x0=4时面积最小,进而求得点P的坐标.
| 1 |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
(2)设A(x1,y1),B(x2,y2),由|FA|=2|FB|,得 x1-2x2=
| 1 |
| 2 |
| 2 |
| k2 |
| 1 |
| 4 |
(3)设P(x0,y0),R(0,b),N(0,c),且b>c,则直线PR的方程可得,由题设知,圆心(1,0)到直线PR的距离为1,把x0,y0代入化简整理可得(x0-2)b2+2y0b-x0=0,同理可得(x0-2)c2+2y0c-x0=0,进而可知b,c为方程(x0-2)x2+2y0x-x0=0的两根,根据求根公式,可求得b-c,进而可得△PRN的面积的表达式,根据均值不等式可知当x0=4时面积最小,进而求得点P的坐标.
解答:解:(1)设抛物线C的方程为y2=2px(p>0),∵
=
,∴p=1,∴抛物线C的方程为y2=2x
(2)设A(x1,y1),B(x2,y2),由|FA|=2|FB|,得 x1-2x2=
,又
,∴k2x2+(k2-2)x+
=0,∴x1+x2=
-1,x1x2=
,∴x1=1,x2=
,k=±
∵△=4-4k2>0,∴-1<k<1,∴k=±
,
(3)设P(x0,y0),R(0,b),N(0,c),且b>c,故直线PR的方程为(y0-b)x-x0y+x0b=0.
由题设知,圆心(1,0)到直线PR的距离为1,即
=1,注意到x0>2,化简上式,得(x0-2)b2+2y0b-x0=0,同理可得(x0-2)c2+2y0c-x0=0,由上可知,b,c为(x0-2)x2+2y0x-x0=0的两根,根据求根公式,可得 b-c=
=
,故△PRN的面积为
S=
( b-c )x0=
=(x0-2 )+
+4≥2
+4=8,等号当且仅当x0=4时成立.此时点P的坐标为 ( 4 , 2
)或 ( 4 , -2
),
综上所述,当点P的坐标为 ( 4 , 2
)或 ( 4 , -2
)时,△PRN的面积取最小值8.
| p |
| 2 |
| 1 |
| 2 |
(2)设A(x1,y1),B(x2,y2),由|FA|=2|FB|,得 x1-2x2=
| 1 |
| 2 |
|
| k2 |
| 4 |
| 2 |
| k2 |
| 1 |
| 4 |
| 1 |
| 4 |
2
| ||
| 3 |
∵△=4-4k2>0,∴-1<k<1,∴k=±
2
| ||
| 3 |
(3)设P(x0,y0),R(0,b),N(0,c),且b>c,故直线PR的方程为(y0-b)x-x0y+x0b=0.
由题设知,圆心(1,0)到直线PR的距离为1,即
| |y0-b+x0b | | ||
|
| ||||||
| x0-2 |
| 2x0 |
| x0-2 |
S=
| 1 |
| 2 |
| ||
| x0-2 |
| 4 |
| x0-2 |
(x0-2 )•
|
| 2 |
| 2 |
综上所述,当点P的坐标为 ( 4 , 2
| 2 |
| 2 |
点评:本题主要考查了抛物线的标准方程和直线与抛物线的关系.直线与圆锥曲线的问题常涉及到圆锥曲线的性质和直线的基本知识点,如直线被圆锥曲线截得的弦长、弦中点问题,垂直问题,对称问题.与圆锥曲线性质有关的量的取值范围等是近几年命题的新趋向.

练习册系列答案
相关题目
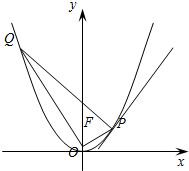 已知抛物线C的顶点在原点,焦点为F(0,1).
已知抛物线C的顶点在原点,焦点为F(0,1).