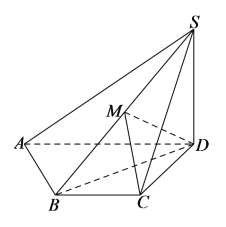
题目内容
【题目】已知椭圆
的离心率为
，且以原点O为圆心，椭圆C的长半轴长为半径的圆与直线
相切．
（1）求椭圆的标准方程；
（2）已知动直线l过右焦点F，且与椭圆C交于A、B两点，已知Q点坐标为
，求
的值．
【答案】（1）
；（2）
．
【解析】
（1）根据椭圆的离心率为
，得到
，根据直线与圆的位置关系，得到原心到直线的距离等于半径，得到
，从而求得
，进而求得椭圆的方程；
（2）分直线的斜率存在是否为0与不存在三种情况讨论，写出直线的方程，与椭圆方程联立，利用韦达定理，向量的数量积，结合已知条件求得结果.
（1）由离心率为，可得
，
，且以原点O为圆心，椭圆C的长半轴长为半径的圆的方程为
，
因与直线
相切，则有
，即，
，
，
故而椭圆方程为．
（2）①当直线l的斜率不存在时，
，
，
由于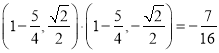
；
②当直线l的斜率为0时，
，
，
则
；
③当直线l的斜率不为0时，设直线l的方程为
，
，
，
由及，
得
，有
，∴
，
，
，
，
∴
，
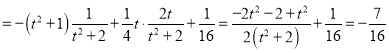综上所述：
．
【题目】某高校共有学生15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300名学生每周平均体育运动时间的样本数据（单位：小时）.
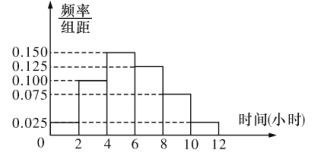
（1）应收集多少位女生的样本数据？
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为：
，
，
，
，
，
，估计该校学生每周平均体育运动时间超过4小时的概率；
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有
的把握认为“该校学生的毎周平均体育运动时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附：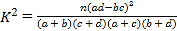
，其中
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【题目】2019年双十一落下帷幕，天猫交易额定格在268（单位：十亿元）人民币（下同），再创新高，比去年218（十亿元）多了50（十亿元）．这些数字的背后，除了是消费者买买买的表现，更是购物车里中国新消费的奇迹，为了研究历年销售额的变化趋势，一机构统计了2010年到2019年天猫双十一的销售额数据y（单位：十亿元），绘制如表：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额y | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图，如图所示
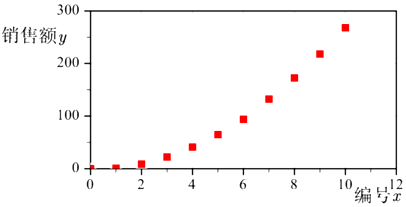
（1）根据散点图判断，
与
哪一个适宜作为销售额
关于
的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果及如表中的数据，建立关于的回归方程，并预测2020年天猫双十一销售额；（注：数据保留小数点后一位）
（3）把销售超过100（十亿元）的年份叫“畅销年”，把销售额超过200（十亿元）的年份叫“狂欢年”，从2010年到2019年这十年的“畅销年”中任取2个，求至少取到一个“狂欢年”的概率．
参考数据：
|
|
|
|
|
|
参考公式：
对于一组数据
，其回归直线
的斜率和截距的最小二乘估计公式分别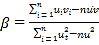
，
．
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数
（个）和温度
（
）的7组观测数据，其散点图如所示：
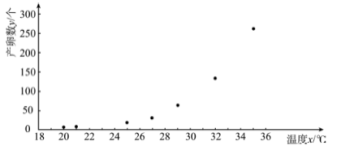
根据散点图，结合函数知识，可以发现产卵数和温度可用方程
来拟合，令
，结合样本数据可知
与温度可用线性回归方程来拟合．根据收集到的数据，计算得到如下值：
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中
，
．
（1）求和温度的回归方程（回归系数结果精确到
）；
（2）求产卵数关于温度的回归方程；若该地区一段时间内的气温在
之间（包括
与
），估计该品种一只昆虫的产卵数的范围.（参考数据：
，
，
，
，
．）
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为
．