题目内容
7.《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜,中斜和大斜,“术”即方法.以S,a,b,c分别表示三角形的面积,大斜,中斜,小斜,ha,hb,hc分别为对应的大斜,中斜,小斜上的高,所以S=$\sqrt{\frac{1}{4}[{a}^{2}×{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}]}$=$\frac{1}{2}$aha=$\frac{1}{2}$bhb=$\frac{1}{2}$chc.已知ha=3,hb=4,hc=6,根据上述公式,可以推理其对应边分别为( )| A. | $\frac{32\sqrt{15}}{15}$,$\frac{8\sqrt{15}}{5}$,$\frac{16\sqrt{15}}{15}$ | B. | $\frac{32}{15}$,$\frac{8}{5}$,$\frac{16}{15}$ | ||
| C. | 4,3,2 | D. | 8,6,4 |
分析 设该三角形的面积为S,a=$\frac{2S}{3}$,b=$\frac{S}{2}$,c=$\frac{S}{3}$,再代入面积公式解出S,进而求得三边之长.
解答 解:设该三角形的面积为S,则有:
S=$\frac{1}{2}$aha=$\frac{1}{2}$bhb=$\frac{1}{2}$chc,且ha=3,hb=4,hc=6,
所以,a=$\frac{2S}{3}$,b=$\frac{S}{2}$,c=$\frac{S}{3}$,
代入公式S=$\sqrt{\frac{1}{4}[{a}^{2}×{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}]}$并平方得,
S2=$\frac{1}{4}$[$\frac{4S^2}{9}$•$\frac{S^2}{4}$-$\frac{1}{4}$•($\frac{4S^2}{9}$+$\frac{S^2}{4}$-$\frac{S^2}{9}$)2],
整理得,4S2=$\frac{S^4}{9}$-$\frac{49S^4}{24^2}$,
解得,S=$\frac{48}{\sqrt{15}}$=$\frac{16\sqrt{15}}{5}$,
所以,a=$\frac{2S}{3}$=$\frac{32\sqrt{15}}{15}$,b=$\frac{S}{2}$=$\frac{8\sqrt{15}}{5}$,c=$\frac{S}{3}$=$\frac{16\sqrt{15}}{15}$,
故选A.
点评 本题主要考查了应用三角形的面积公式求三角形的三边长,具有一定的运算技巧,属于中档题.

练习册系列答案
相关题目
16.数列{an}中,a1=2,a2=1,且$\frac{1}{a_n}+\frac{1}{{{a_{n+2}}}}=\frac{2}{{{a_{n+1}}}}$(n∈N*),则a6等于( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
17.在△ABC中,若sinA:sinB:sinC=3:4:6,则cosC=( )
| A. | $\frac{11}{24}$ | B. | $\frac{13}{24}$ | C. | -$\frac{13}{24}$ | D. | -$\frac{11}{24}$ |
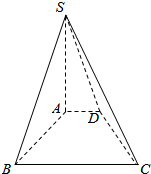 已知四棱锥S-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD.
已知四棱锥S-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD.