题目内容
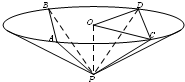
顶点为P的圆锥的轴截面积是等腰直角三角形,A是底面圆周上的点,O为底面圆的圆心,AB⊥OB,垂足为B,OH⊥PB,垂足为H,且PA=4,C为PA的中点,则当三棱锥O-HPC的体积最大时,OB的长是( )A.

B.

C.

D.

【答案】分析:画出图形,说明PC是三棱锥P-OCH的高,△OCH的面积在OH=HC= 时取得最大值,求出OB即可.
时取得最大值,求出OB即可.
解答: 解:AB⊥OB,可得PB⊥AB,即AB⊥面POB,所以面PAB⊥面POB.
解:AB⊥OB,可得PB⊥AB,即AB⊥面POB,所以面PAB⊥面POB.
OH⊥PB,则OH⊥面PAB,OH⊥HC,OH⊥PC,
又,PC⊥OC,所以PC⊥面OCH.即PC是三棱锥P-OCH的高.PC=OC=2.
而△OCH的面积在OH=HC= 时取得最大值(斜边=2的直角三角形).
时取得最大值(斜边=2的直角三角形).
当OH= 时,由PO=2
时,由PO=2 ,知∠OPB=30°,OB=POtan30°=
,知∠OPB=30°,OB=POtan30°= .
.
故选D.
点评:本题考查圆锥的结构特征,棱锥的体积等知识,考查空间想象能力,是中档题.
 时取得最大值,求出OB即可.
时取得最大值,求出OB即可.解答:
 解:AB⊥OB,可得PB⊥AB,即AB⊥面POB,所以面PAB⊥面POB.
解:AB⊥OB,可得PB⊥AB,即AB⊥面POB,所以面PAB⊥面POB.OH⊥PB,则OH⊥面PAB,OH⊥HC,OH⊥PC,
又,PC⊥OC,所以PC⊥面OCH.即PC是三棱锥P-OCH的高.PC=OC=2.
而△OCH的面积在OH=HC=
 时取得最大值(斜边=2的直角三角形).
时取得最大值(斜边=2的直角三角形).当OH=
 时,由PO=2
时,由PO=2 ,知∠OPB=30°,OB=POtan30°=
,知∠OPB=30°,OB=POtan30°= .
.故选D.
点评:本题考查圆锥的结构特征,棱锥的体积等知识,考查空间想象能力,是中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 (2013•安徽)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,
(2013•安徽)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,