题目内容
给出下列五个命题:
(1)函数y=-sin(kπ+x)(k∈Z)是奇函数;
(2)函数f(x)=tanx的图象关于点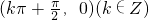 对称;
对称;
(3)函数f(x)=sin|x|是最小正周期为π的周期函数;
(4)设θ是第二象限角,则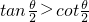 ,且
,且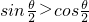 ;
;
(5)函数y=cos2x+sinx的最小值是-1.
其中正确的命题是
- A.(1)、(2)、(3)
- B.(1)、(2)、(5)
- C.(1)、(5)
- D.(1)、(3)、(4)
B
分析:(1)先由诱导公式对函数y=-sin(kπ+x)化简,然后在检验函数的奇偶性即可
(2)根据正切函数的性质可知函数f(x)=tanx的图象得对称中心
(3)由函数f(x)=sin|x|的图象可知该函数不是周期函数
(4)由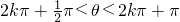 ,则
,则 <
<
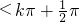 ,k∈Z,分k为偶数,k为奇数两种情况检验
,k∈Z,分k为偶数,k为奇数两种情况检验
(5)由y=cos2x+sinx=-sin2x+sinx+1=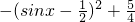 ,sinx∈[-1,1],结合二次函数的性质可求
,sinx∈[-1,1],结合二次函数的性质可求
解答:(1)由诱导公式可得,函数y=-sin(kπ+x)=(-1)ksinx,满足奇函数,故(1)正确
(2)根据正切函数的性质可知函数f(x)=tanx的图象关于点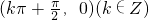 对称,故 (2)正确
对称,故 (2)正确
(3)由函数f(x)=sin|x|的图象可知该函数不是周期函数,故(3)错误
(4)设θ是第二象限角即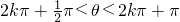 ,则
,则 <
<
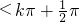 ,k∈Z
,k∈Z
当k为偶数,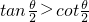 ,
,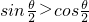 成立,
成立,
当k为奇数时,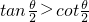 ,
,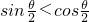 ,故(3)错误
,故(3)错误
(5)函数y=cos2x+sinx=-sin2x+sinx+1=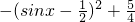 ,sinx∈[-1,1]
,sinx∈[-1,1]
则当sinx=-1时,函数有最小值-1,故(5)正确
故选:B
点评:本题主要考查了三角函数的性质的判断,解题的关键是要熟练掌握三角函数的性质并能灵活应用,其中(3)中的函数的周期的判断的方法是根据函数的图象,而不要利用周期定义.
分析:(1)先由诱导公式对函数y=-sin(kπ+x)化简,然后在检验函数的奇偶性即可
(2)根据正切函数的性质可知函数f(x)=tanx的图象得对称中心
(3)由函数f(x)=sin|x|的图象可知该函数不是周期函数
(4)由
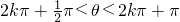 ,则
,则 <
<
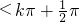 ,k∈Z,分k为偶数,k为奇数两种情况检验
,k∈Z,分k为偶数,k为奇数两种情况检验(5)由y=cos2x+sinx=-sin2x+sinx+1=
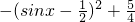 ,sinx∈[-1,1],结合二次函数的性质可求
,sinx∈[-1,1],结合二次函数的性质可求解答:(1)由诱导公式可得,函数y=-sin(kπ+x)=(-1)ksinx,满足奇函数,故(1)正确
(2)根据正切函数的性质可知函数f(x)=tanx的图象关于点
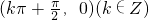 对称,故 (2)正确
对称,故 (2)正确(3)由函数f(x)=sin|x|的图象可知该函数不是周期函数,故(3)错误
(4)设θ是第二象限角即
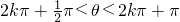 ,则
,则 <
<
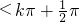 ,k∈Z
,k∈Z当k为偶数,
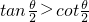 ,
,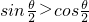 成立,
成立,当k为奇数时,
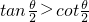 ,
,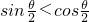 ,故(3)错误
,故(3)错误(5)函数y=cos2x+sinx=-sin2x+sinx+1=
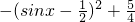 ,sinx∈[-1,1]
,sinx∈[-1,1]则当sinx=-1时,函数有最小值-1,故(5)正确
故选:B
点评:本题主要考查了三角函数的性质的判断,解题的关键是要熟练掌握三角函数的性质并能灵活应用,其中(3)中的函数的周期的判断的方法是根据函数的图象,而不要利用周期定义.

练习册系列答案
相关题目